Корелационният и регресионният анализ могат да се използват за изследване на връзката между променливите, докато анализите от типа на Т-тест и ANOVA изследват разликите между групите.
Корелационният анализ показва връзката на всяка променлива с всяка друга поотделно. Коефициентът на връзката между променливите може да бъде както отрицателен, така и положителен. За разлика от регресионния анализ, между променливите не може да има причинно-следствена връзка.
За този пример ще използваме набор от данни от извадките на SPSS: customer_dbase.sav
Изберете customer_dbase.sav.
Щракнете върху раздела Analyze (Анализ) от горното меню.
Намерете раздела Correlate (Корелация) в раздела Analyze (Анализ). След това щракнете върху бутона Bivariate Correlations.
След като кликнете, ще видите следното меню:

Предположението за нормалност е важно за корелационния анализ. Така че, ако променливите ви са нормално разпределени, трябва да използвате коефициента на корелация на Пиърсън, а ако не, използвайте коефициента на Спирман.
Ако приемете, че между променливите има само еднопосочна връзка (т.е. очаквате само положителна връзка между променливите), трябва да изберете One-tailed test. Ако не сте сигурни или не предвиждате положителна или отрицателна връзка, изберете Two-tailed test.
След като приключите, щракнете върху OK, за да видите резултатите. За този пример избрахме коефициентите на Пиърсън и Спирмън.
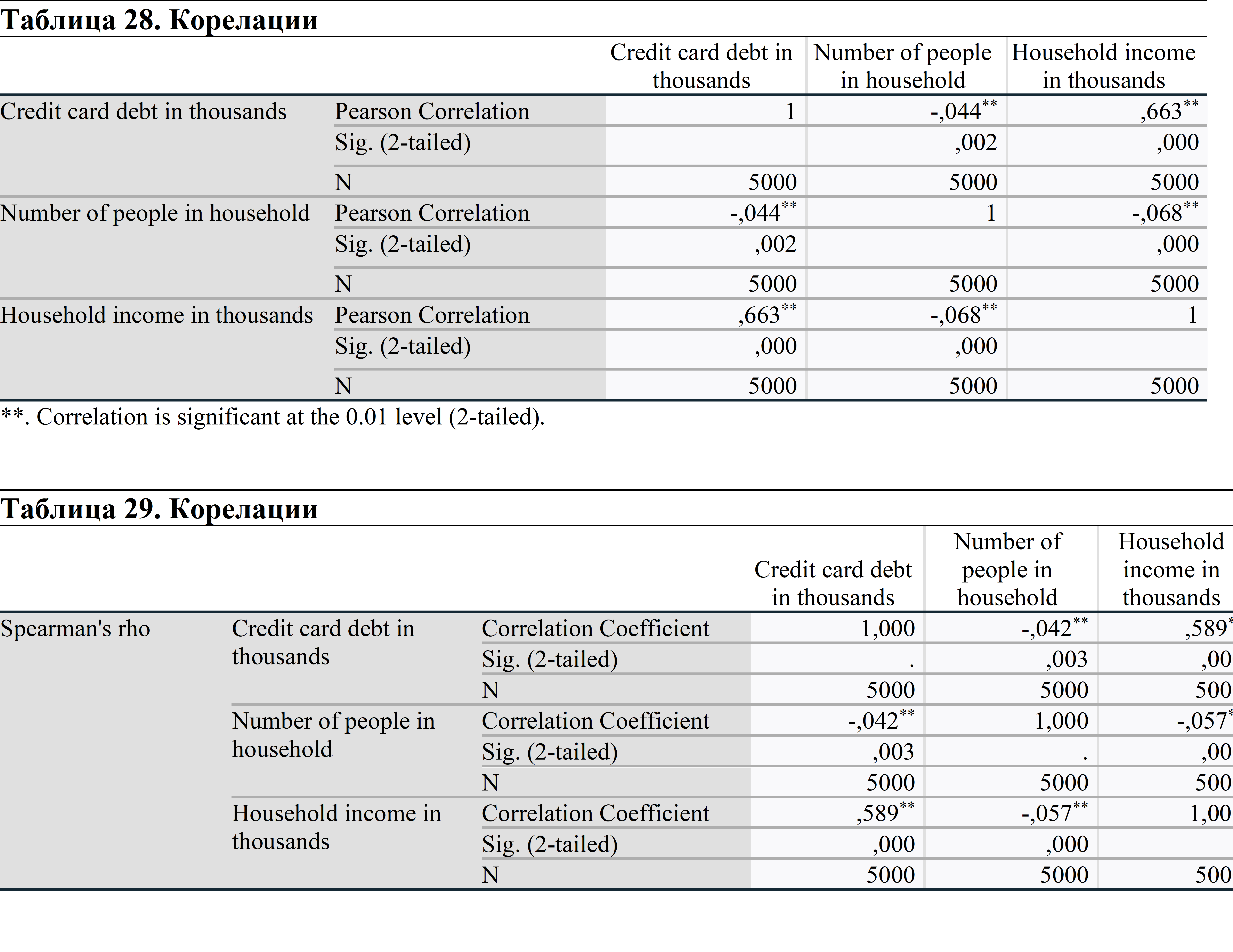
Знакът ** до коефициентите показва, че корелацията е значима на ниво 0,01.
Ако знакът е *, това означава, че корелацията е значима при ниво 0,05.
И при двата теста на коефициентите се наблюдава статистически значима връзка между всяка двойка променливи.
Резултатите от анализа показват, че съществува отрицателна корелация между дълга по кредитна карта и броя на хората в домакинството и положителна корелация между дълга по кредитна карта и дохода на домакинството. Можем да тълкуваме, че домакинствата генерират повече приходи, отколкото харчат. Това е причината за наличието на такава връзка.
Регресионният анализ може да се използва за изследване на ефекта на независимата(ите) променлива(и) върху зависимата променлива. Една проста регресионна функция може да се илюстрира по следния начин:
Yi = ß0 + ß1x + ɛ
И: Зависима променлива
ß0: константа / пресечна точка
ß1: Наклон / Коефициент
x: Независима променлива
ɛ: Член за грешка
В анализа може да има повече от една независима променлива. Влиянието на всяка променлива върху зависимата променлива може да се изследва с техните коефициенти. Ненаблюдаваните ефекти и променливи ще бъдат представени от члена на грешката.
За този пример ще използваме набор от данни от извадките на SPSS: customer_dbase.sav
Изберете customer_dbase.sav.
Щракнете върху раздела Analyze (Анализ) от горното меню.
Намерете раздела Regression (Регресия) в раздел Analyze (Анализиране). След това щракнете върху бутона Linear.

В този пример ще направим множествен регресионен анализ. Ще разгледаме влиянието на нивото на образование, категориите работни места и членството в профсъюзи върху доходите на домакинствата.
Преди да започнем, искам да ви напомня, че променливите ви трябва да са нормално разпределени и да имат еднаква дисперсия.

Изберете Model fit (Прилягане на модела), descriptives (Описания), part and partial correlations (Частични и непълни корелации), colinearity diagnostics (Диагностика на колинеарността), confidence intervals (като 95%) и щракнете върху Continue (Продължи).
В главното меню щракнете върху OK, за да продължите с анализа.
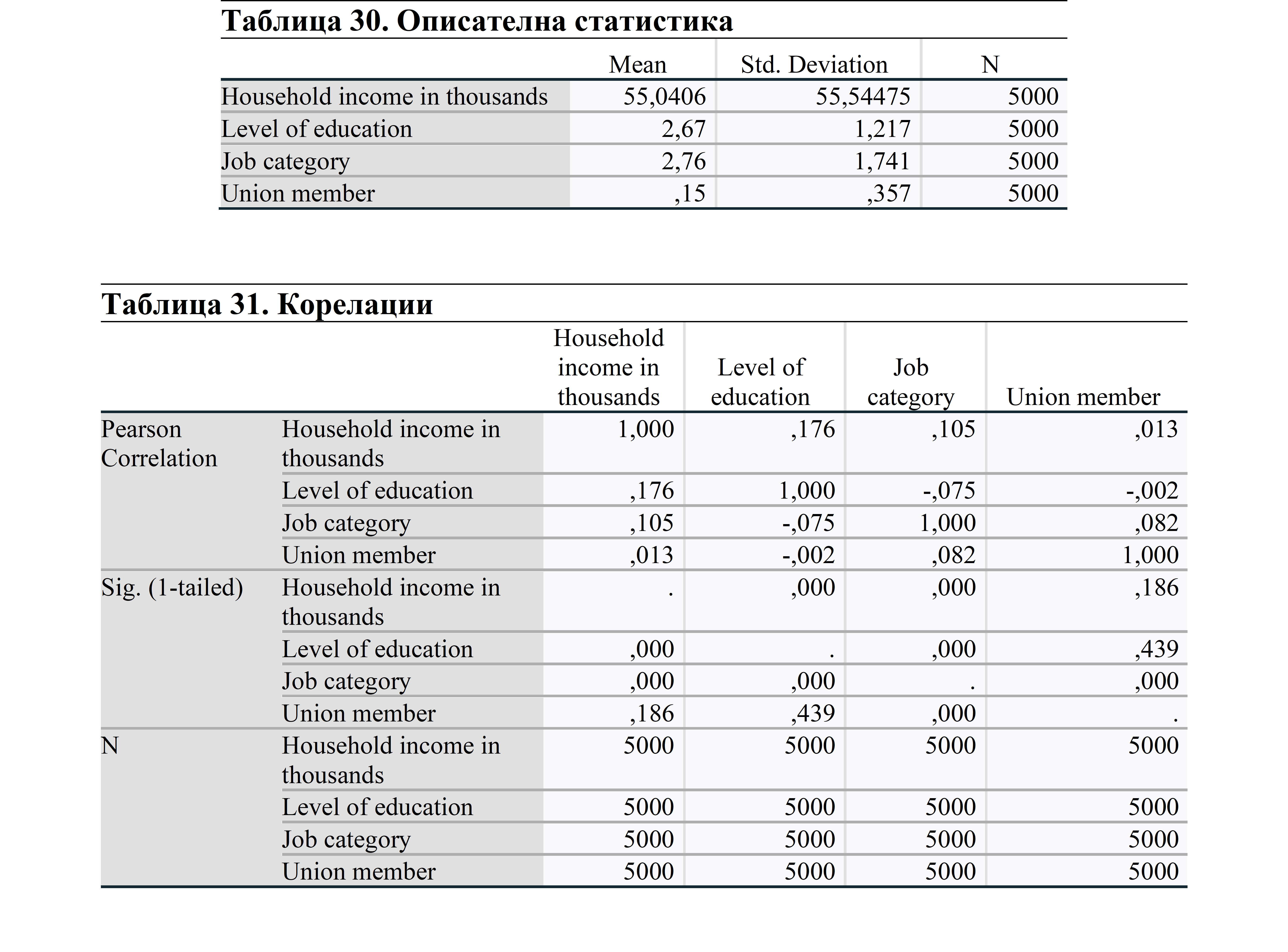
В корелационната матрица е важно да няма връзка над 0,70. Това показва силна връзка между променливите и дава неверни резултати. Това би означавало проблем с мултиколинеарността. При този анализ виждаме, че няма силна връзка между променливите. Така че можем да продължим с анализа.

Обобщението на модела показва стойностите на R. Тъй като сме използвали модел на множествена регресия, трябва да проверим коригирания R Square. Тази стойност показва силата на независимите променливи да обяснят зависимата променлива. И така, от нивото на образование, категорията на работа и членството в профсъюз могат да бъдат обяснени само 4,4 % от дохода на домакинството. Това означава, че има и други фактори, които в момента не можем да наблюдаваме и използваме в модела. Ако имате повече променливи, трябва да ги използвате в регресионния модел, в противен случай анализът ще бъде повлиян от ненаблюдавани променливи.

Когато проверихме Sig. (p-стойността) на анализа ANOVA, се вижда, че тя е по-ниска от 0,05. Това означава, че поне една променлива сред независимите променливи има статистически значим ефект върху зависимата променлива. За повече информация относно ефекта ще разгледаме следващия анализ.
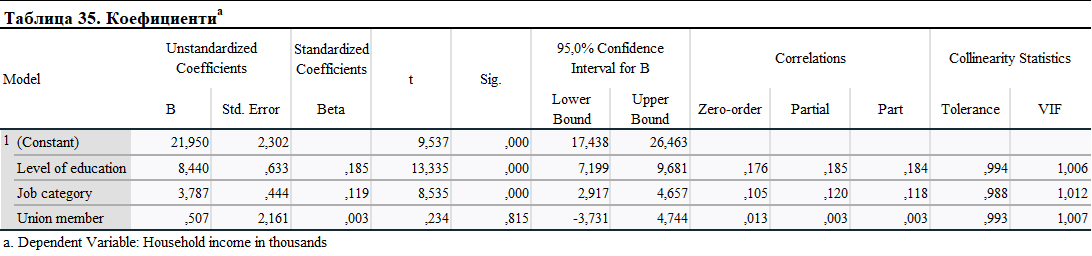
Първото нещо, което трябва да проверим в тази таблица, е Sig. (p-стойност). Вижда се, че нивото на образование и категорията на работа имат значителен ефект върху дохода на домакинството, от друга страна, членството в профсъюз няма статистически значимо влияние върху него.
Нестандартизираните коефициенти показват ефекта от увеличението с една единица върху доходите на домакинствата. Така че увеличението с една единица на нивото на образование и категорията на работа увеличава доходите на домакинствата с 8 440 и 3 787 USD.
Стандартизираните коефициенти показват ефекта от увеличаването на стандартното отклонение с една единица върху стандартното отклонение на доходите на домакинствата.









