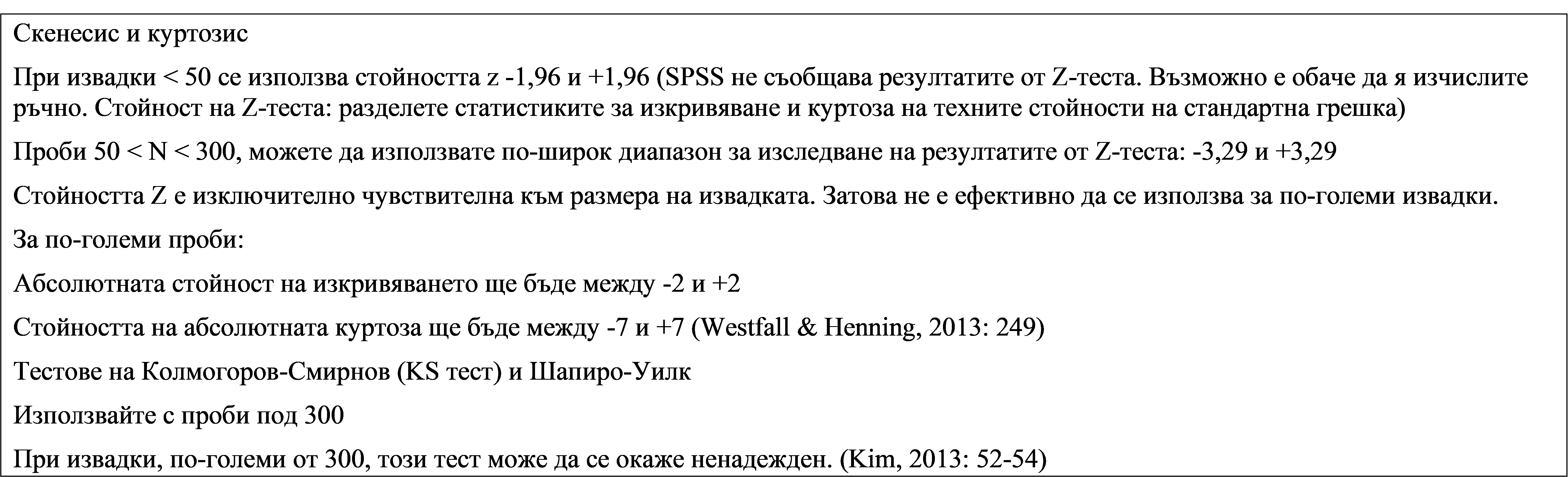Резюме:
Разбиране на предположението за нормалност в статистическия анализ, неговото значение и методите за оценка на нормалността.
Цели на обучението:
Разберете концепцията за нормалност в статистическия анализ.
Да научат различни методи за оценка на нормалността, като графични методи и статистически тестове.
Разпознайте последиците от нарушаването на предположението за нормалност в инференциалната статистика.
Нормалността е едно от най-важните допускания при анализа тип ANOVA. Затова е важно да се провери дали всяка променлива в анализа има нормално разпределение.
Съществуват няколко мерки и показатели, които можете да използвате, за да проверите предположението за нормалност.
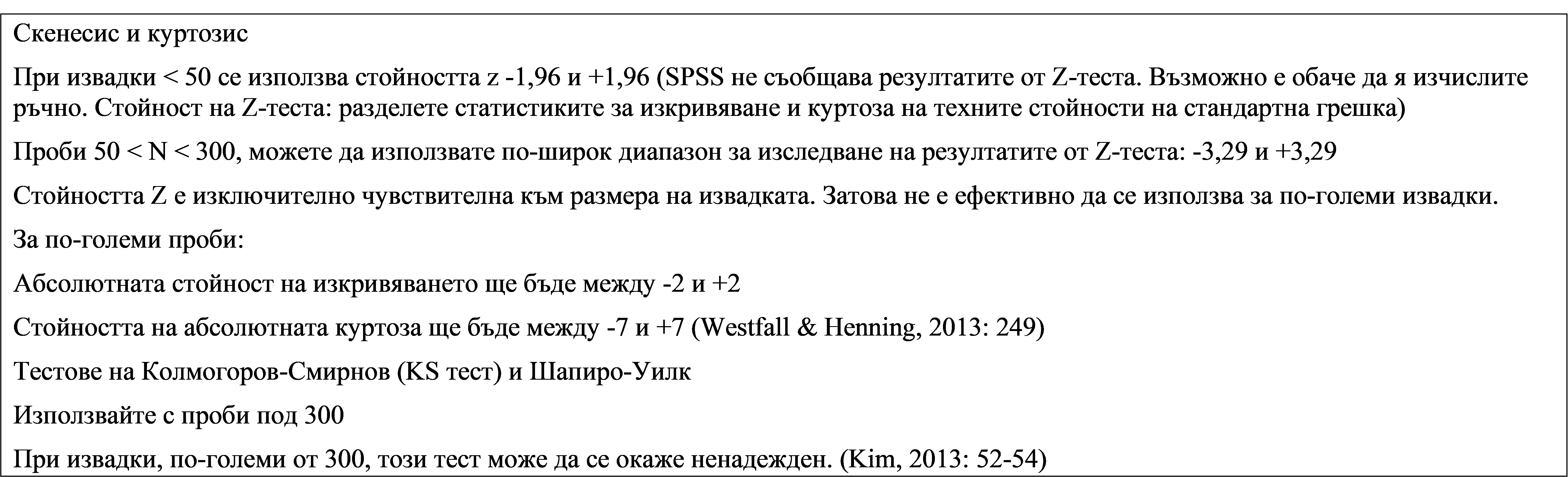
Нулевата хипотеза на двата теста е, че данните са нормално разпределени. Така че p-стойностите трябва да са по-високи от 0,05, за да можем да приемем нулевата хипотеза. Въпреки това, ако извадките са повече от 300, трябва да се вземат предвид стойностите на изкривяването и куртозата.
Да упражним теста за нормалност!
Изберете cross_sell.sav
Щракнете върху бутона Analyze (Анализиране) в горното меню. След това отидете на Descriptive Statistics (Описателна статистика) и щракнете върху бутона Explore (Разглеждане).
Изберете следните променливи и ги включете в списъка със зависими променливи:
Покупки със специална оферта [buyoff]
Покупки на CD [buycd]
Покупки на книги [buybk]
Отстъпка за CD клуба [disccd]
Отстъпка за книжния клуб [discbk]
Регистър на отстъпката в CD клуба [lndisccd]
Дневник за отстъпка в книжния клуб [lndiscbk]
След това щракнете върху бутона Plots в дясното меню.
Щракнете върху Хистограма под заглавието Descriptive (Описателни) и изберете също Normality plots with tests (Нормални графики с тестове). След това щракнете върху бутона Продължи.
В главното меню щракнете върху OK, за да извършите тестовете и да видите резултатите.
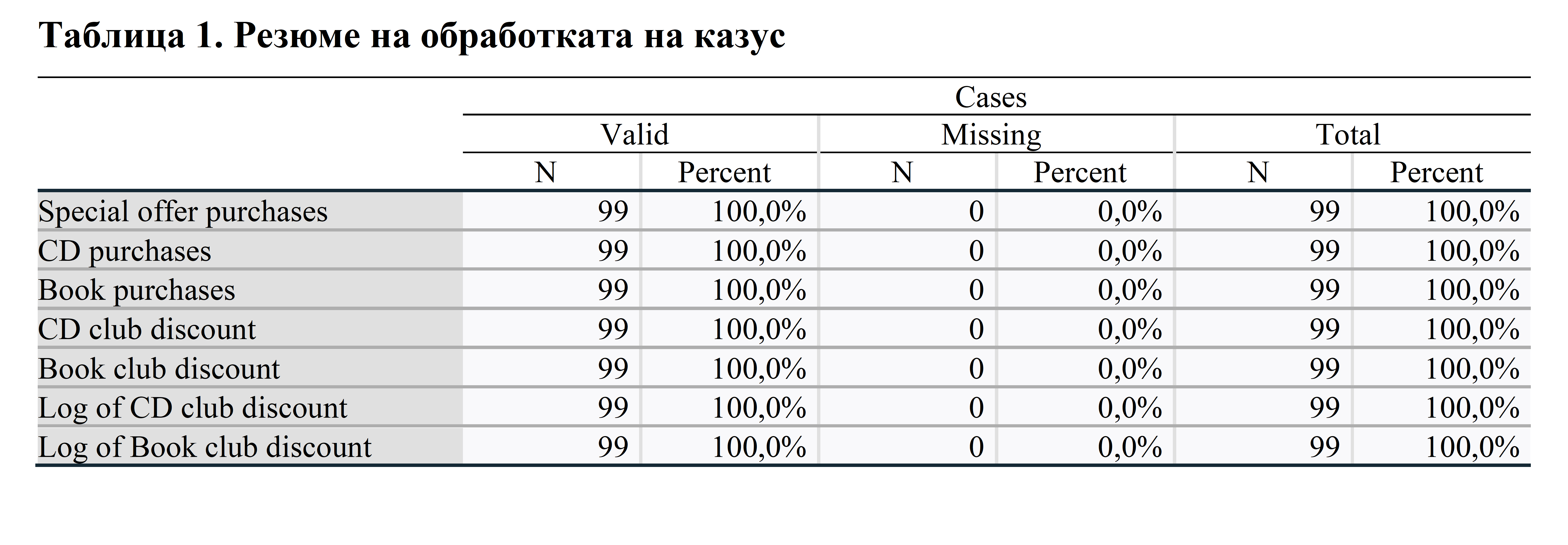
Когато разгледаме описателната статистика за променливите:
Променлива: Покупки по специална оферта
Изкривяване: Статистика: 0.01 Стандартна грешка: 0,243 - Стойност на Z-теста: 0,01 / 0,243 = 0,041
Куртоза Статистика: -0.313 Стандартна грешка: 0,481 - Стойност на Z-теста: -0,313 / 0,481 = -0,65
Променлива: Покупки на компактдискове
Изкривяване: Статистика: 0.237 Стандартна грешка: 0,243 - Стойност на Z-теста: 0,237 / 0,243 = 0,975
Куртоза: Статистика: 0.099 Стандартна грешка: 0,481 - Стойност на Z-теста: 0,099 / 0,481 = 0,203
Променлива: Покупки на книги
Изкривяване: Статистика: -0.194 Стандартна грешка: 0,243 - Стойност на Z-теста: -0,194 / 0,243 = -0,798
Куртоза: Статистика: -0.177 Стандартна грешка: 0,481 - Стойност на Z-теста: -0,177 / 0,481 = -0,368
Променлива: Отстъпка от CD клуба
Изкривяване: Статистика: 0.615 Стандартна грешка: 0,243 - Стойност на Z-теста: 0,615 / 0,243 = 2,53
Куртоза: Статистика: -0.778 Стандартна грешка: 0,481 - Стойност на Z-теста: -0,778 / 0,481 = -1,617
Променлива: Отстъпка за книжен клуб
Изкривяване: Статистика: 0.682 Стандартна грешка: 0,243 - Стойност на Z-теста: 0,682 / 0,243 = 2,81
Куртоза: Статистика: -0.425 Стандартна грешка: 0,481 - Стойност на Z-теста: -0,425 / 0,481 = -0,88
Променлива: Логистична стойност на отстъпката в CD клуба
Изкривяване: Статистика: -0.332 Стандартна грешка: 0,243 - Стойност на Z-теста: -0,332 / 0,243 = -1,37
Куртоза: Статистика: -1.095 Стандартна грешка: 0,481 - Стойност на Z-теста: -1,095 / 0,481 = -2,28
Променлива: Логистична стойност на отстъпката в книжния клуб
Изкривяване: Статистика: -0.407 Стандартна грешка: 0,243 - Стойност на Z-теста: -0,407 / 0,243 = -1,674
Куртоза: Статистика: -0.870 Стандартна грешка: 0,481 - Стойност на Z-теста: -0,870 / 0,481 = -1,808
Тъй като броят N на всяка променлива е 99, е възможно да се проверят стойностите на Z-теста в интервала от -3,29 до +3,29. Следователно може да се каже, че всички променливи са нормално разпределени.
Трябва обаче да се потърсят и резултатите от теста за нормалност. Резултатите от тестовете на Колмогоров-Смирнов и Шапиро-Уилк показват, че покупките на специални оферти, покупките на компактдискове и покупките на книги са нормално разпределени, тъй като тяхната Sig. (p-стойност) е по-голяма от 0,05. За останалите променливи трябва да отхвърлим нулевата хипотеза. Когато се разглеждат и двата теста, въпреки че стойностите на p се различават, те дават последователни резултати.
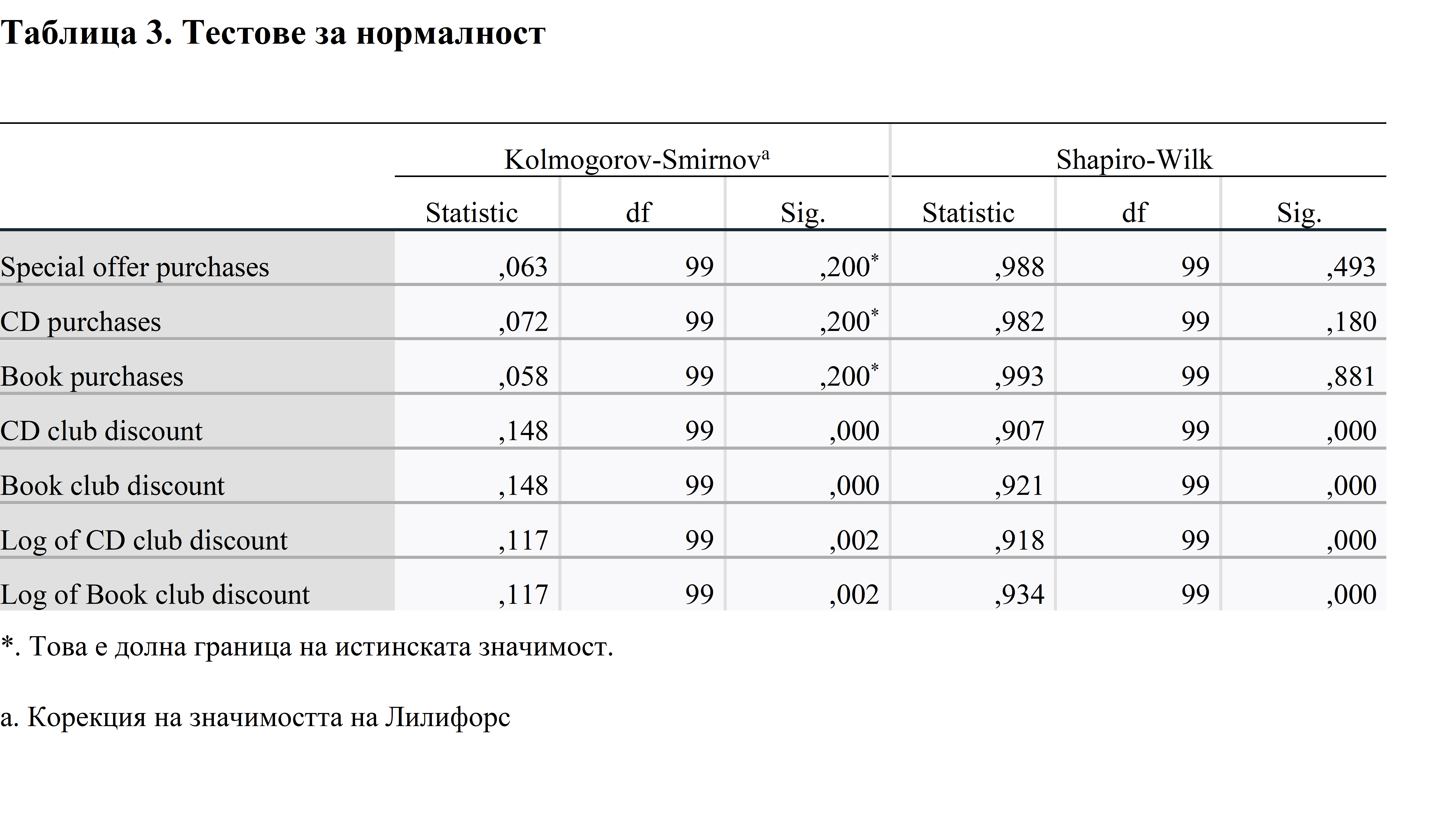
Възможно е също така да се провери разпределението по хистограма на променливите. Ето един пример за идеално нормално разпределение:
Източник: https://www.mathsisfun.com/data/standard-normal-distribution.html (Достъп: 01.06.2023 г.)
Когато се разглеждат хистограмите, се вижда, че хистограмите на първите три променливи, за които е установено, че са нормално разпределени според резултатите от теста за нормалност, са по-близки до идеалния пример за нормално разпределение. Хистограмите на останалите променливи започват с висока честота, която постепенно намалява и/или се колебае.
