Resumo:
Compreender o pressuposto da normalidade na análise estatística, a sua importância e os métodos para avaliar a normalidade.
Objectivos de aprendizagem:
Compreender o conceito de pressuposto de normalidade em análise estatística.
Aprender diferentes métodos para avaliar a normalidade, tais como métodos gráficos e testes estatísticos.
Reconhecer as implicações da violação do pressuposto da normalidade na estatística inferencial.
A normalidade é um dos pressupostos mais importantes na análise do tipo ANOVA. Assim, é importante verificar se cada variável na análise tem uma distribuição normal.
Existem várias medidas e indicadores que você pode usar para verificar o pressuposto de normalidade.
A hipótese nula de ambos os testes é que os dados são normalmente distribuídos. Assim, os valores de p devem ser superiores a 0,05, para que possamos aceitar a hipótese nula. No entanto, se as amostras forem superiores a 300, devem ser considerados os valores de assimetria e curtose.
Vamos praticar o teste de normalidade!
Selecione cross_sell.sav
Clique no botão Analisar no menu superior. Em seguida, vá para Estatística Descritiva e clique no botão Explorar.
Selecione as seguintes variáveis e coloque-as na lista de dependentes:
Compras em ofertas especiais [buyoff]
Compras de CD [buycd]
Compra de livros [buybk]
CD club desconto [disccd]
Desconto clube de livros [discbk]
Log de desconto CD club [lndisccd]
Log de desconto do clube do livro [lndiscbk]
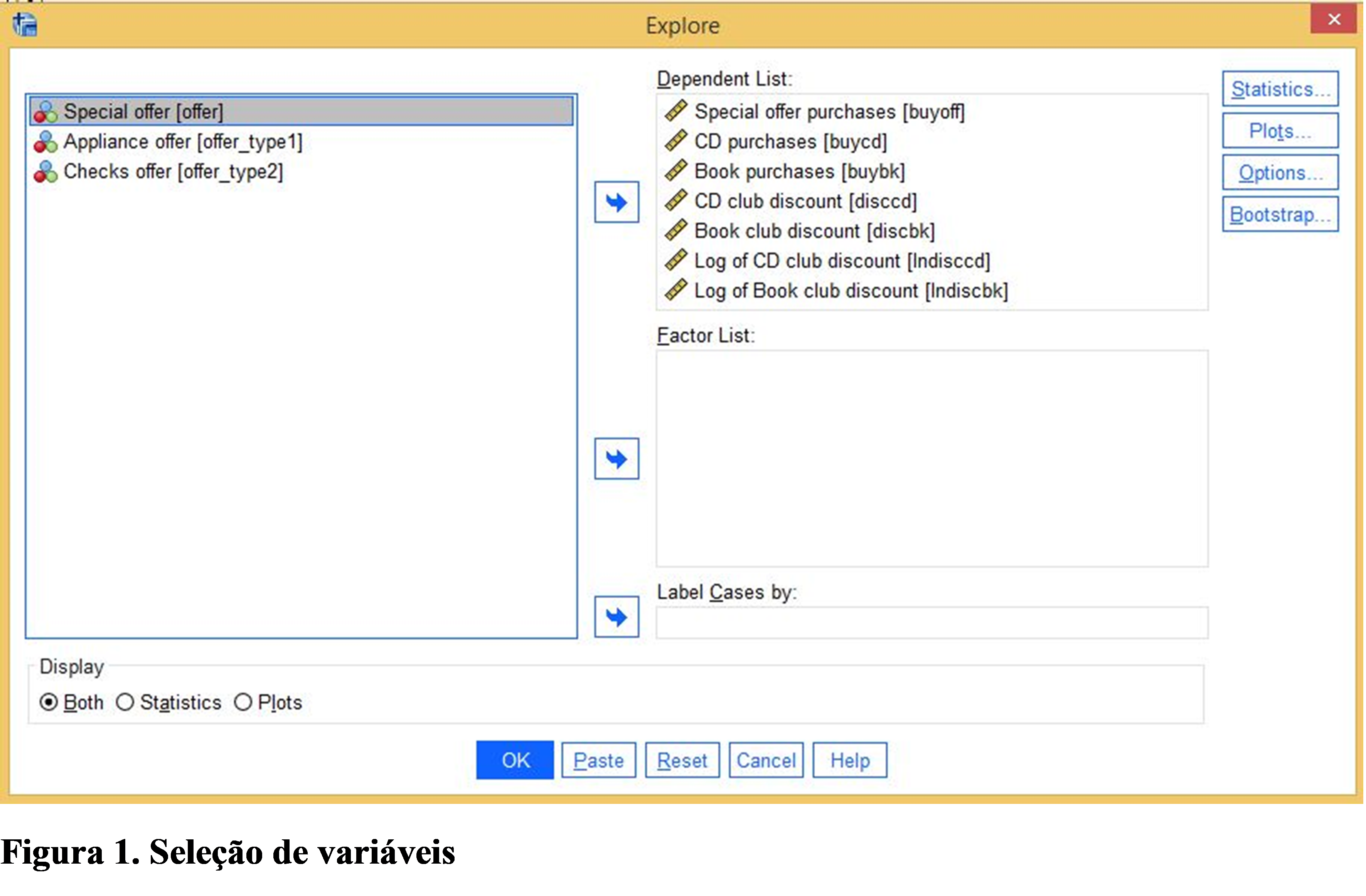
Depois disso, clique no botão Plots no menu à direita.
Clique em Histograma sob o título Descritivo e também selecione Gráficos de normalidade com testes. Depois disso, clique no botão Continuar.
No menu principal, clique em OK para realizar os testes e ver os resultados.
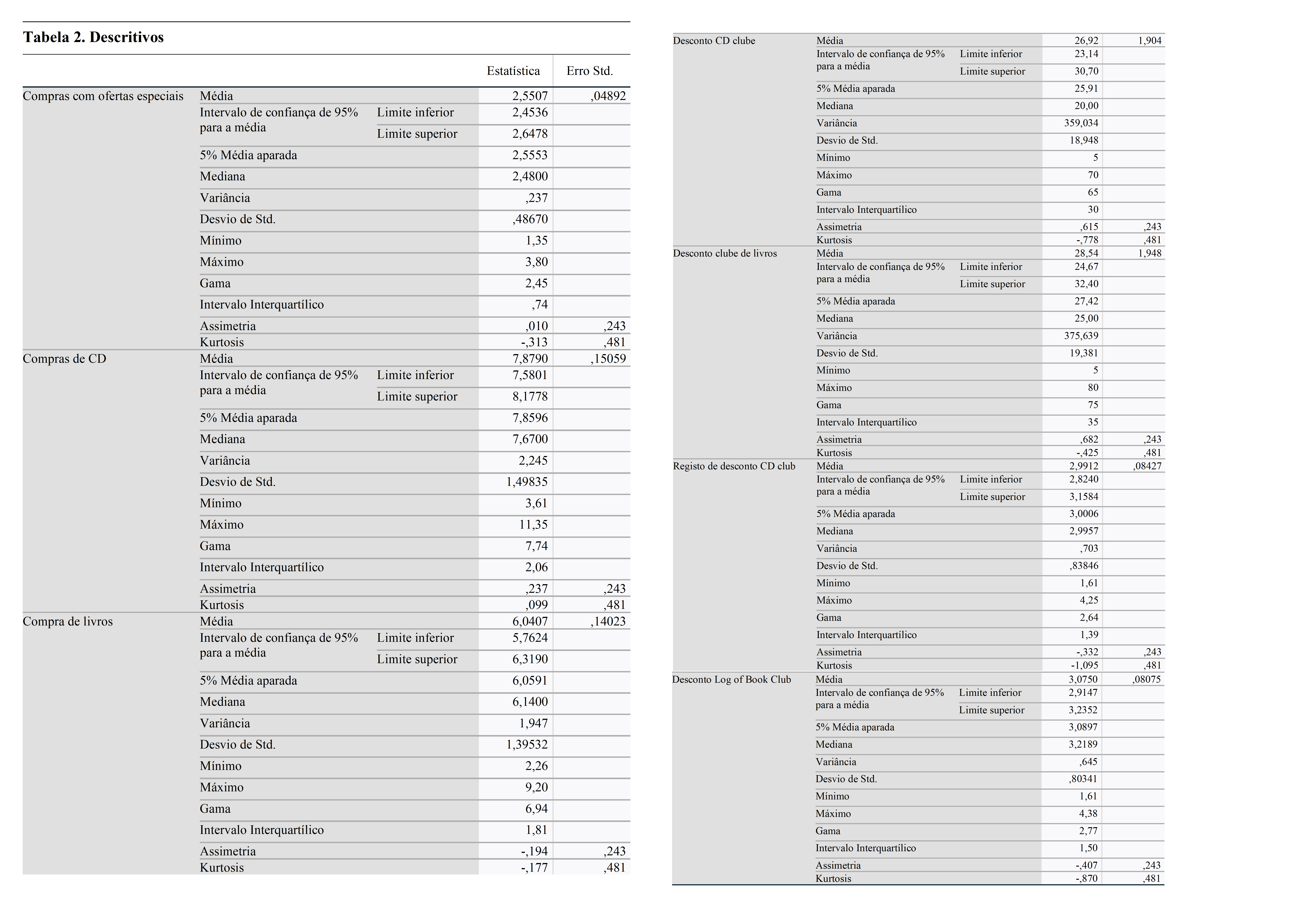
Quando examinamos a estatística descritiva para variáveis:
Variável: Compras com ofertas especiais
Assimetria: Estatística: 0,01 Erro padrão: 0,243 – Valor do teste Z: 0,01 / 0,243 = 0,041
Estatística Kurtosis: -0,313 Erro padrão: 0,481 – Valor do teste Z: -0,313 / 0,481 = -0,65
Variável: Compras de CD
Assimetria: Estatística: 0,237 Erro padrão: 0,243 – Valor do teste Z: 0,237 / 0,243 = 0,975
Kurtosis: Estatística: 0,099 Erro padrão: 0,481 – Valor do teste Z: 0,099 / 0,481 = 0,203
Variável: Compras de livros
Assimetria: Estatística: -0,194 Erro padrão: 0,243 – Valor do teste Z: -0,194 / 0,243 = -0,798
Kurtosis: Estatística: -0,177 Erro padrão: 0,481 – Valor do teste Z: -0,177 / 0,481 = -0,368
Variável: desconto CD club
Assimetria: Estatística: 0,615 Erro padrão: 0,243 – Valor do teste Z: 0,615 / 0,243 = 2,53
Kurtosis: Estatística: -0,778 Erro padrão: 0,481 – Valor do teste Z: -0,778 / 0,481 = -1,617
Variável: Desconto do clube de livros
Assimetria: Estatística: 0,682 Erro padrão: 0,243 – Valor do teste Z: 0,682 / 0,243 = 2,81
Kurtosis: Estatística: -0,425 Erro padrão: 0,481 – Valor do teste Z: -0,425 / 0,481 = -0,88
Variável: Registo de desconto CD club
Assimetria: Estatística: -0,332 Erro padrão: 0,243 – Valor do teste Z: -0,332 / 0,243 = -1,37
Kurtosis: Estatística: -1.095 Erro padrão: 0.481 – Valor do teste Z: -1.095 / 0.481 = -2.28
Variável: Desconto Log of Book Club
Assimetria: Estatística: -0,407 Erro padrão: 0,243 – Valor do teste Z: -0,407 / 0,243 = -1,674
Kurtosis: Estatística: -0,870 Erro padrão: 0,481 – Valor do teste Z: -0,870 / 0,481 = -1,808
Já o número de N de cada variável é 99. É possível verificar os valores do teste Z no intervalo de -3,29 e +3,29. Portanto, pode-se dizer que todas as variáveis são normalmente distribuídas.
No entanto, também temos de procurar resultados de testes de normalidade. Os resultados dos testes de Kolmogorov-Smirnov e Shapiro-Wilk mostram que as compras de ofertas especiais, compras de CD e compras de livros são normalmente distribuídas, uma vez que o seu Sig. Para o resto das variáveis, temos que rejeitar a hipótese nula. Quando ambos os testes são examinados, mesmo que os valores de p difiram, eles produzem resultados consistentes.
Também é possível verificar a distribuição a partir do histograma das variáveis. Aqui está um exemplo de distribuição normal perfeita:
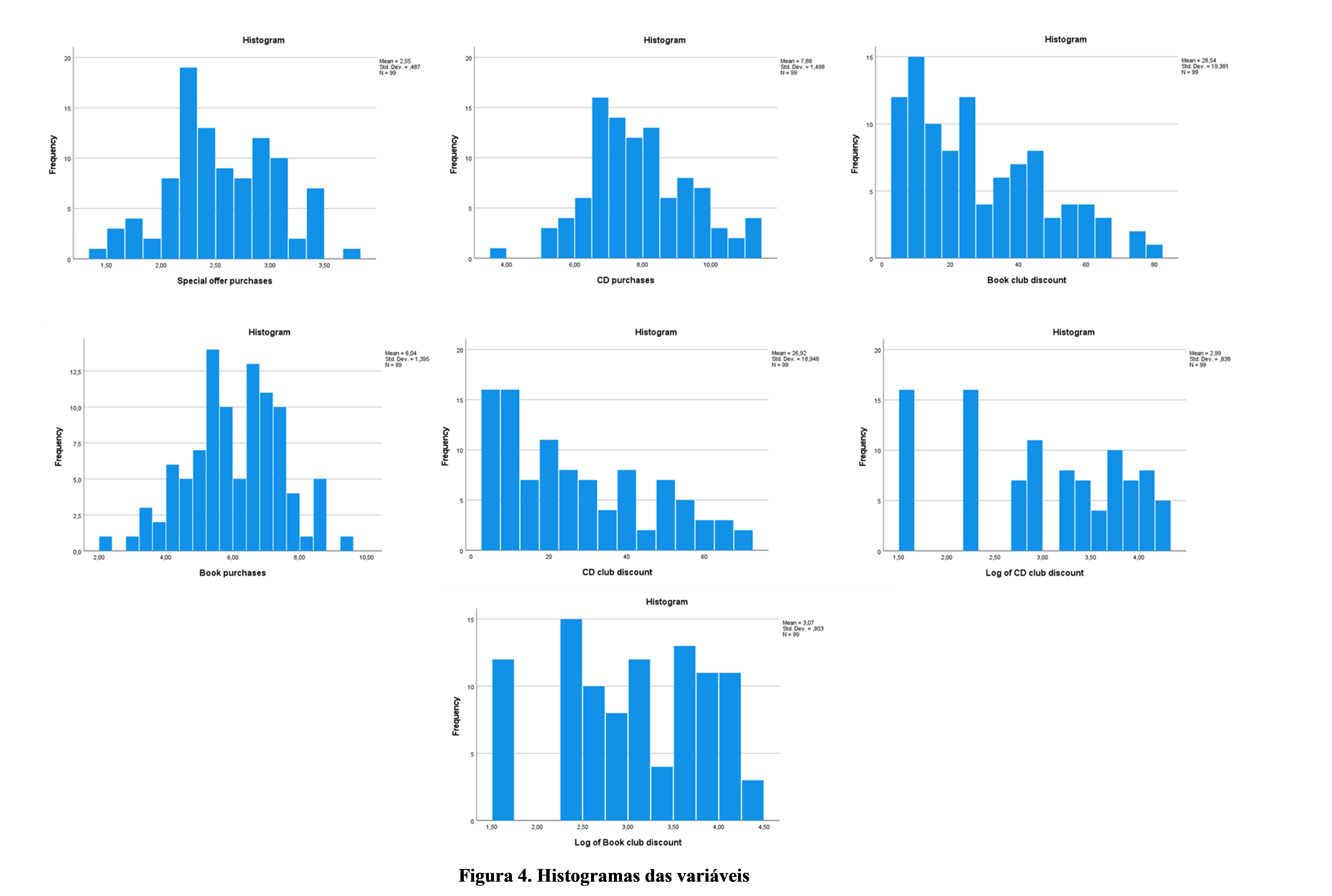
Quando os histogramas são examinados, pode-se ver que os histogramas das 3 primeiras variáveis que são encontradas para ser normalmente distribuído de acordo com os resultados do teste de normalidade, são mais semelhantes com o exemplo perfeito de distribuição normal. Os histogramas das restantes variáveis começam com uma frequência elevada que diminui gradualmente e/ou por flutuação.
