Resumo:
Prática com análise de correlação e regressão utilizando SPSS.
Objetivos de Aprendizagem:
Adquirir experiência prática na condução de análises de correlação e regressão e interpretação de resultados utilizando o SPSS.
Saber como avaliar relações entre variáveis usando análise de correlação e construir modelos preditivos usando análise de regressão.
Praticar a interpretação dos resultados das análises de correlação e regressão e a elaboração de conclusões com base nos resultados.
As análises de correlação e regressão podem ser usadas para examinar a relação entre as variáveis, enquanto as análises do teste T e do tipo ANOVA examinam as diferenças entre os grupos.
A análise de correlação mostra a relação de cada variável entre si separadamente. O coeficiente da relação da variável pode ser negativo ou positivo. Ao contrário da análise de regressão, pode não haver uma causalidade entre as variáveis.
Para este exemplo, usaremos o conjunto de dados de exemplos SPSS: customer_dbase.sav
Selecione customer_dbase.sav.
Clique na seção Analisar no menu superior.
Encontre a seção Correlacionar em Analisar. Em seguida, clique no botão Correlações Bivariadas.
Depois de clicar, você verá o seguinte menu:
Figura 24. Seleção de variáveis
O pressuposto de normalidade é importante para a análise de correlação. Assim, se suas variáveis são normalmente distribuídas, você precisa usar o coeficiente de correlação de pearson, se não usar o coeficiente de spearman.
Se você assumir que há apenas uma relação de uma maneira entre as variáveis (ou seja, você espera apenas uma relação positiva entre as variáveis), você precisa escolher o teste unicaudal. Se você não tem certeza ou não prevê relação positiva ou negativa, escolha Teste bicaudal.
Quando terminar, clique em OK para ver os resultados. Para este exemplo, selecionamos os Coeficientes de Pearson e Spearman.
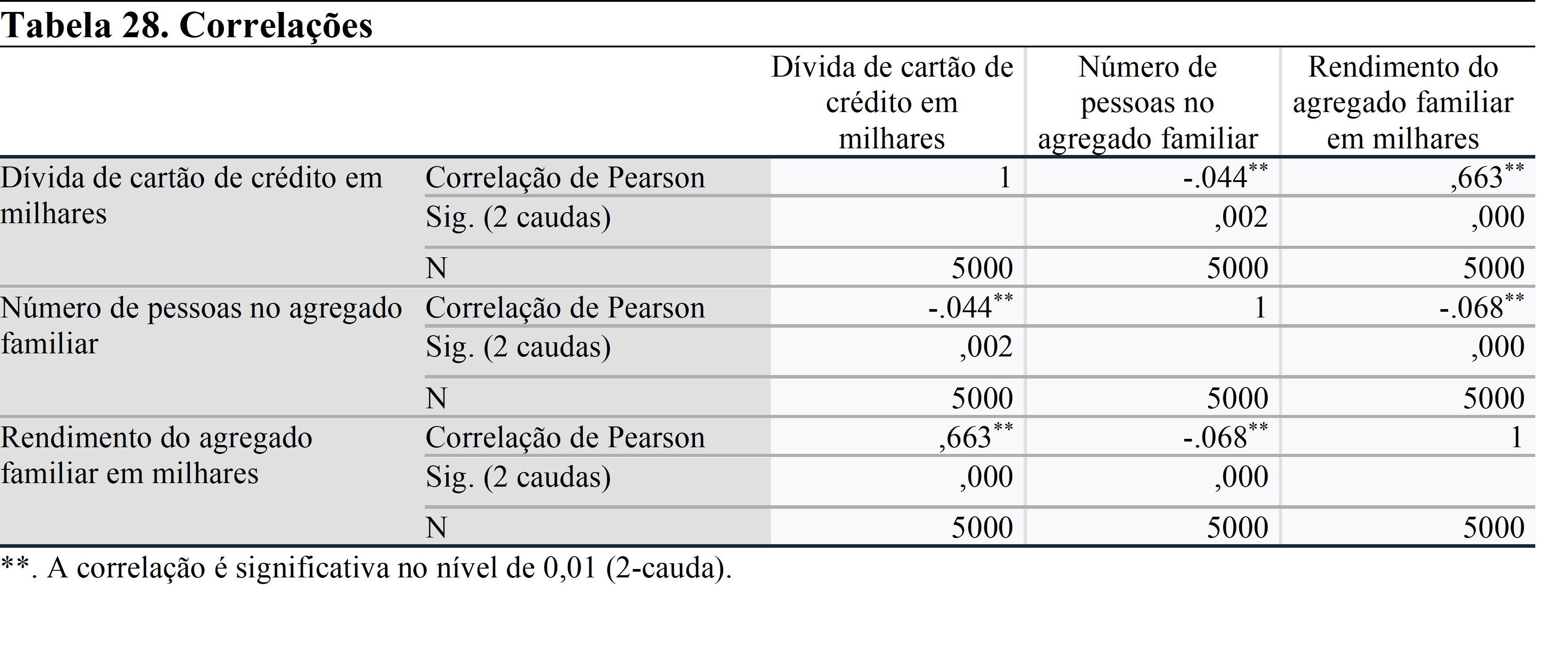
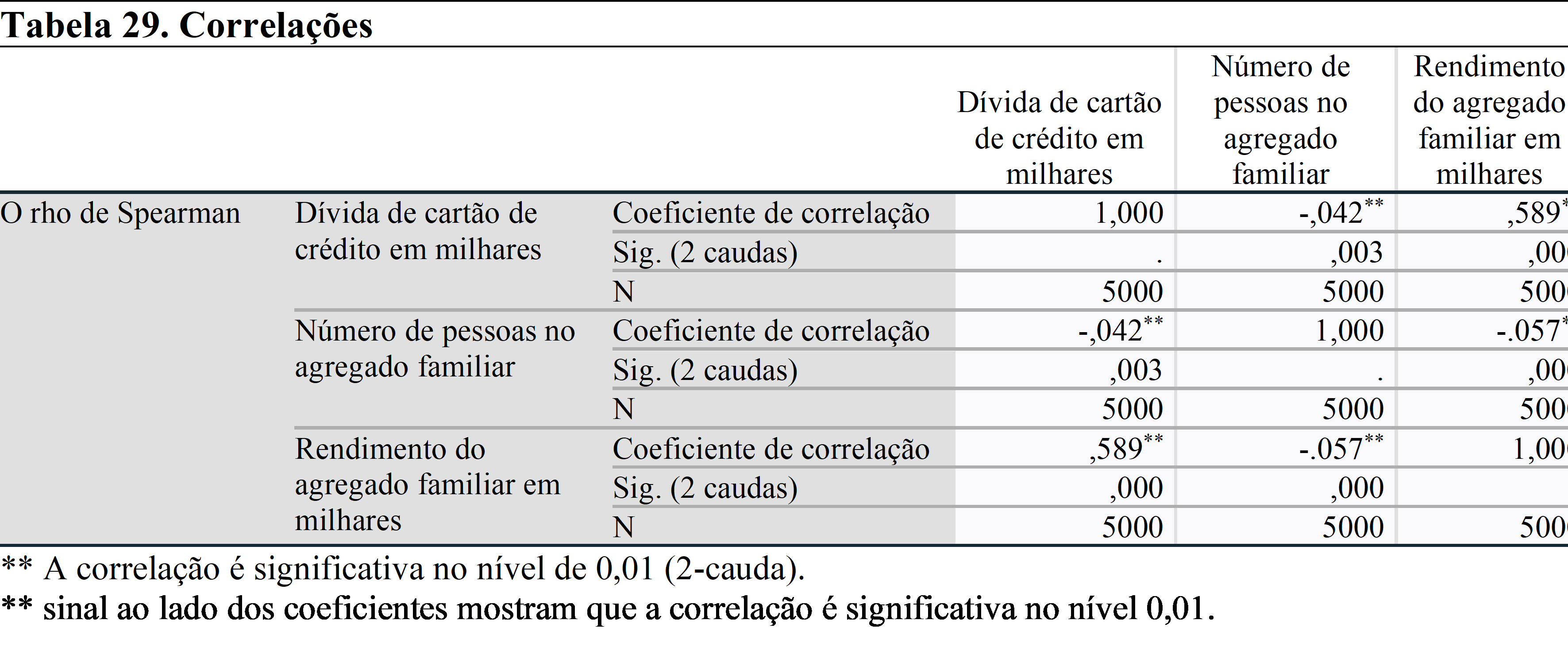
Se o sinal fosse *, isso significaria que a correlação é significativa no nível de 0,05.
Em ambos os testes de coeficientes, há relação estatisticamente significativa entre cada par de variáveis.
Os resultados da análise mostram que existe uma correlação negativa entre a dívida do cartão de crédito e o número de pessoas no agregado familiar, e uma correlação positiva entre a dívida do cartão de crédito e o rendimento do agregado familiar. Podemos insinuar que as famílias geram mais rendimento do que gastaram. Essa é a razão pela qual existe essa relação.
A análise de regressão pode ser usada para examinar o efeito da(s) variável(es) independente(s) sobre a variável dependente. Uma função de regressão simples pode ser ilustrada da seguinte forma:
Yi = ß0 + ß1x + ɛ
Yi: Variável dependente
ß0: Constante / Intercetação
ß1: Declive / Coeficiente
x: Variável independente
ɛ: Termo de erro
Pode haver mais de uma variável independente na análise. Os efeitos de cada variável sobre a variável dependente podem ser examinados com seus coeficientes. Os efeitos e variáveis não observados serão representados pelo termo de erro.
Para este exemplo, usaremos o conjunto de dados de exemplos SPSS: customer_dbase.sav
Selecione customer_dbase.sav.
Clique na seção Analisar no menu superior.
Encontre a seção Regressão em Analisar. Em seguida, clique no botão Linear.
Depois de clicar, você verá o seguinte menu:
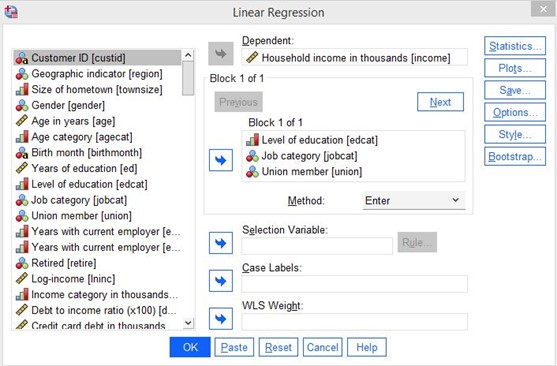
Figura 25: Seleção de variáveis
Neste exemplo, faremos uma análise de regressão múltipla. Examinaremos os efeitos do nível de educação, das categorias profissionais e da filiação sindical na renda familiar.
Antes de começarmos, gostaria de lembrar que, suas variáveis devem ser normalmente distribuídas e ter igual variância.
Depois de selecionar as variáveis, clique no botão Estatísticas à direita:
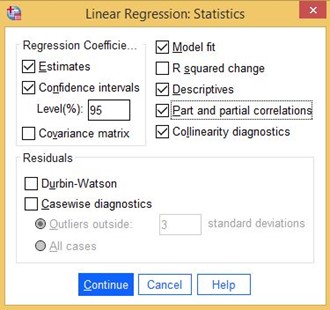
Figura 26: Estatísticas e especificações
Selecione Ajuste do modelo, descritivos, correlações parciais e parciais, diagnósticos de colinearidade, intervalos de confiança (como 95%) e clique em Continuar.
No menu principal, clique em OK para continuar a análise.
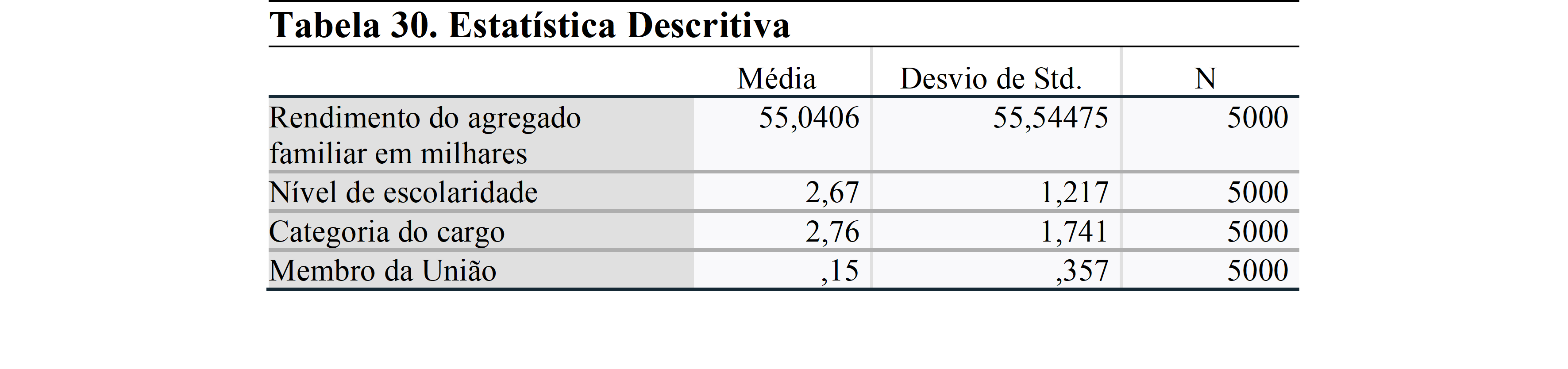
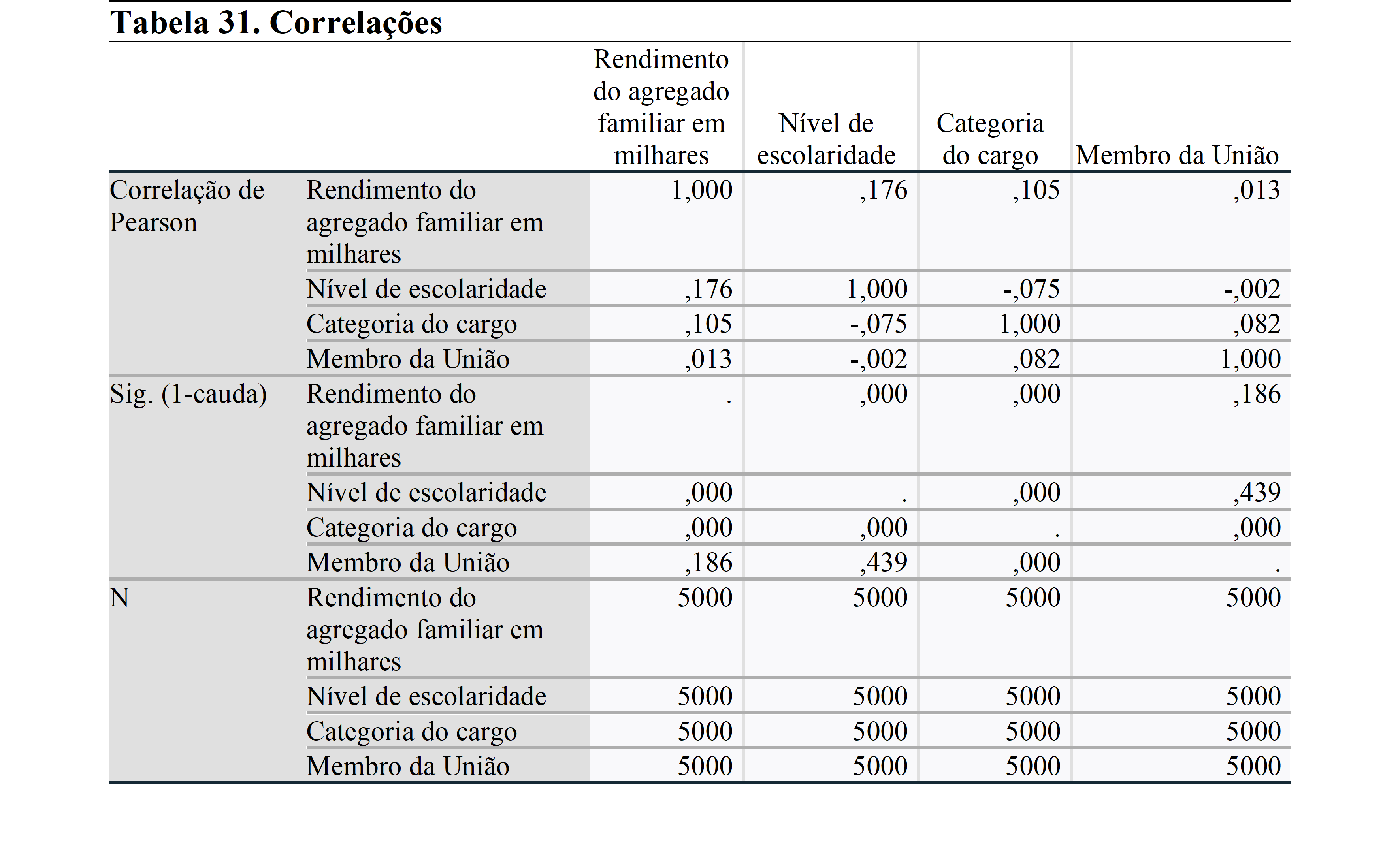
Na matriz de correlação, é importante não ter uma relação acima de 0,70. Isso indica uma forte relação entre as variáveis e produz resultados espúrios. Isso indicaria um problema de multicolinearidade. Nesta análise, vemos que não há uma forte relação entre as variáveis. Assim, podemos continuar a analisar.
O resumo do modelo mostra os valores R. Como usamos um modelo de regressão múltipla, precisamos verificar o R Quadrado Ajustado. Este valor mostra o poder das variáveis independentes para explicar a variável dependente. Assim, a partir do nível de escolaridade, categoria profissional e filiação sindical, apenas 4,4% da renda familiar pode ser explicada. Isso significa que existem outros contribuintes que atualmente não podemos observar e usar no modelo. Se você tiver mais variáveis, você precisa usá-lo no modelo de regressão, caso contrário, a análise será efetuada por variáveis não observadas.
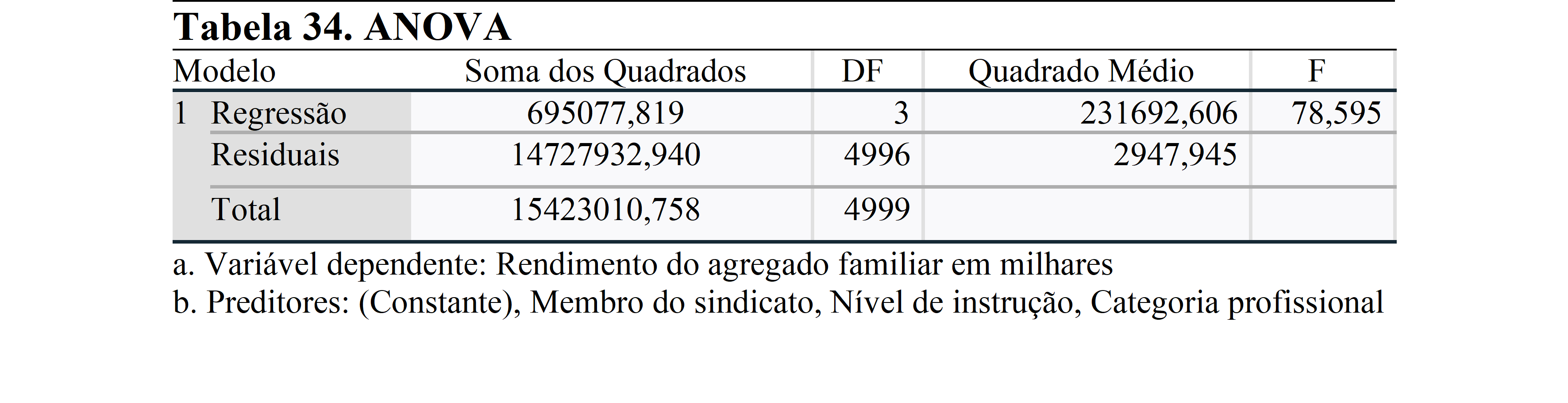
Quando verificamos o Sig. (p-valor) da análise ANOVA, observa-se que é inferior a 0,05. Isto significa que pelo menos uma variável entre as variáveis independentes tem um efeito estatisticamente significativo sobre a variável dependente. Para obter mais informações sobre o efeito, examinaremos a próxima análise.
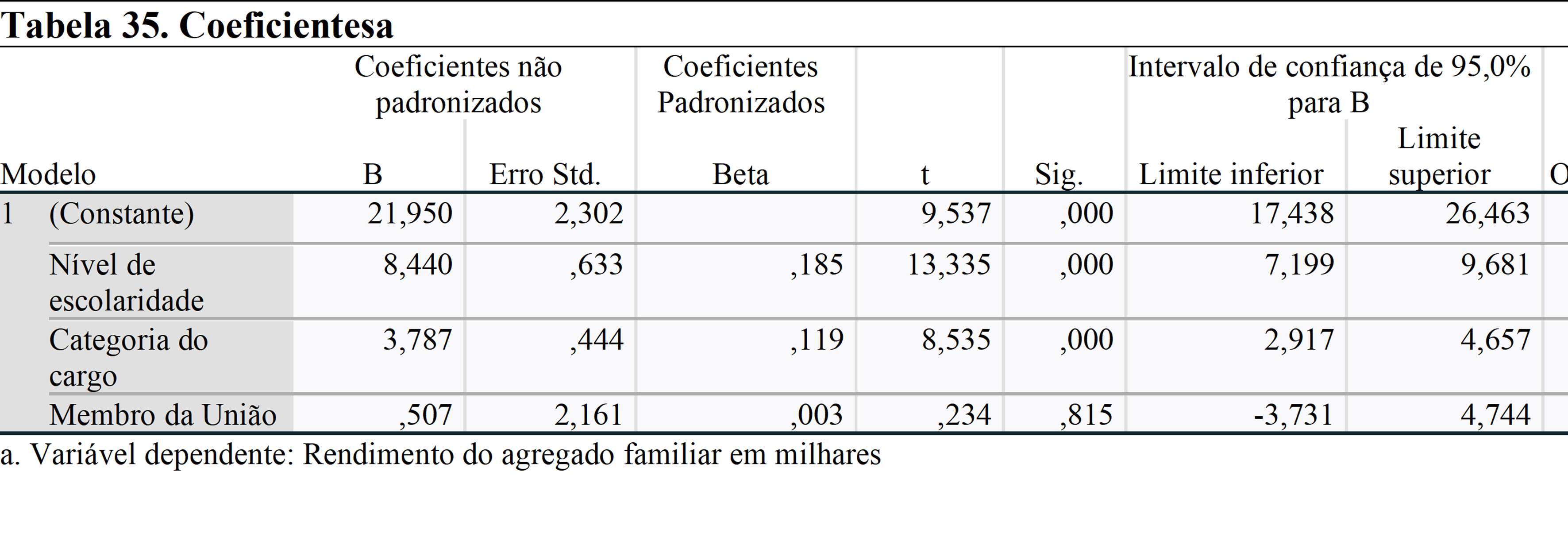
A primeira coisa que precisamos verificar nesta tabela é Sig. (valor p). Observa-se que o nível de escolaridade e a categoria profissional têm um efeito significativo sobre a renda familiar, por outro lado, ser membro de um sindicato não tem impacto estatisticamente significativo sobre ela.
Coeficientes não padronizados mostram o efeito de um aumento unitário na renda familiar. Assim, um aumento de nível no nível de educação e categoria de emprego aumentar a renda familiar em 8.440 e 3.787 USD.
Os Coeficientes Padronizados mostram o efeito do aumento de uma unidade no desvio padrão sobre o desvio padrão da renda familiar.
