Rezumat:
Practică practică cu analiza de corelație și regresie utilizând SPSS.
Obiective de învățare:
1. Înțelegerea conceptului de analiză a corelației și a utilizării sale în examinarea relațiilor între variabile.
2. Învățarea despre diferiți coeficienți de corelație, cum ar fi coeficientul de corelație Pearson și coeficientul de corelație rang Spearman.
3. Identificarea situațiilor în care analiza corelației este aplicabilă și interpretarea corectă a coeficienților de corelație.
Analizele de corelație și regresie pot fi utilizate pentru a examina relația dintre variabile, în timp ce testul T și analizele de tip ANOVA examinează diferențele dintre grupuri.
Analiza corelației arată relația fiecărei variabile între ele separat. Coeficientul relației variabilei poate fi negativ sau pozitiv. Spre deosebire de analiza de regresie, este posibil să nu existe o cauzalitate între variabile.
Pentru acest exemplu vom folosi setul de date din eșantioanele SPSS: customer_dbase.sav
Selectați customer_dbase.sav.
Faceți clic pe secțiunea Analiză din meniul de sus.
Găsiți secțiunea Corelare sub Analiză. Apoi faceți clic pe butonul Corelații bivariate.
După ce ați făcut clic, veți vedea următorul meniu:
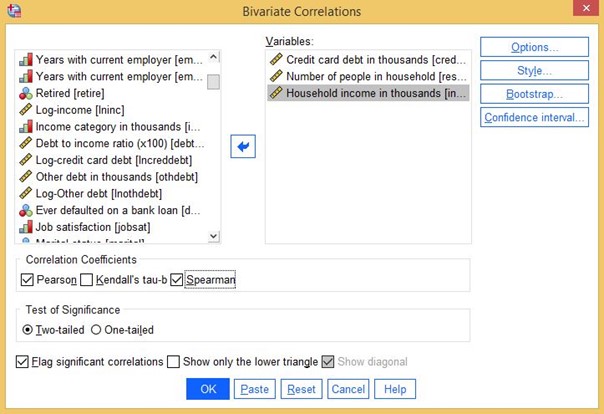
Figura 24. Selecție variabilă
Ipoteza de normalitate este importantă pentru analiza corelației. Deci, dacă variabilele tale sunt distribuite în mod normal, trebuie să folosești coeficientul de corelație Pearson, dacă nu să folosești coeficientul spearman.
Dacă presupuneți că există o singură relație între variabile (adică vă așteptați doar la o relație pozitivă între variabile), trebuie să alegeți testul cu o singură coadă. Dacă nu sunteți sigur sau nu prevedeți o relație pozitivă sau negativă, alegeți Testul cu două cozi.
După ce ați terminat, faceți clic pe OK pentru a vedea rezultatele. Pentru acest exemplu, am selectat atât coeficienții Pearson, cât și cei Spearman.
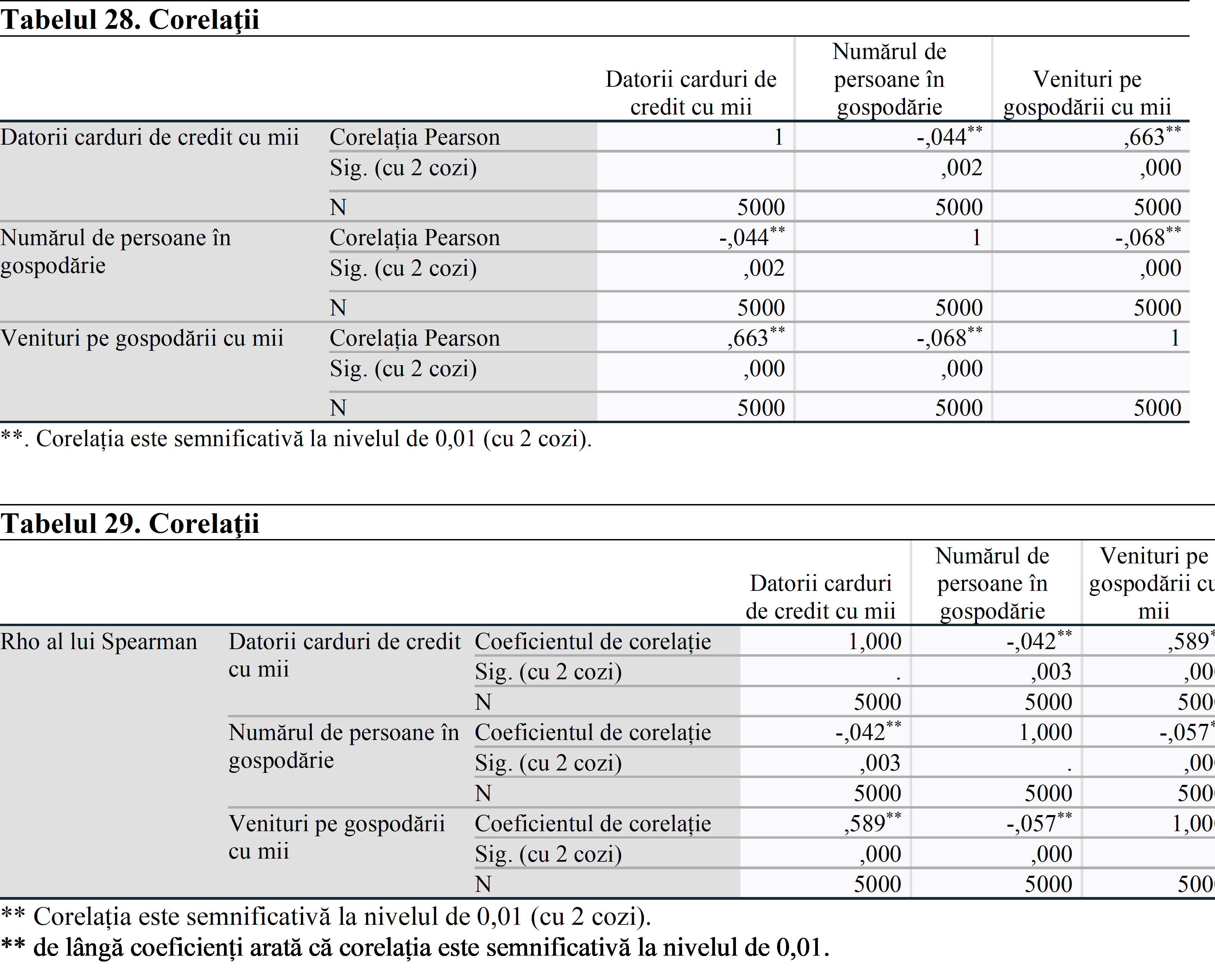
Dacă semnul ar fi *, ar însemna că corelația este semnificativă la nivelul de 0,05.
În ambele teste de coeficienț, există o relație semnificativă statistic între fiecare pereche de variabile.
Rezultatele analizei arată că există o corelație negativă între datoria cardului de credit și numărul de persoane din gospodărie și o corelație pozitivă între datoria cardului de credit și venitul gospodăriei. Putem pretinde că gospodăria generează mai multe venituri decât a cheltuit. Acesta este motivul pentru care există o astfel de relație.
Analiza de regresie poate fi utilizată pentru a examina efectul variabilei independente asupra variabilei dependente. O funcție simplă de regresie poate fi ilustrată după cum urmează:
Yi = ß0 + ß1x + ɛ
Yi: Variabilă dependentă
ß0: Constantă / Interceptare
ß1: Pantă / Coeficient
x: Variabilă independentă
ɛ: Termen de eroare
Pot exista mai multe variabile independente în analiză. Efectele fiecărei variabile asupra variabilei dependente pot fi examinate cu coeficienții lor. Efectele și variabilele neobservate vor fi reprezentate de termenul de eroare.
Pentru acest exemplu vom folosi setul de date din eșantioanele SPSS: customer_dbase.sav
Selectați customer_dbase.sav.
Faceți clic pe secțiunea Analiză din meniul de sus.
Găsiți secțiunea Regresie sub Analiză. Apoi faceți clic pe butonul Liniar.
După ce ați făcut clic, veți vedea următorul meniu:
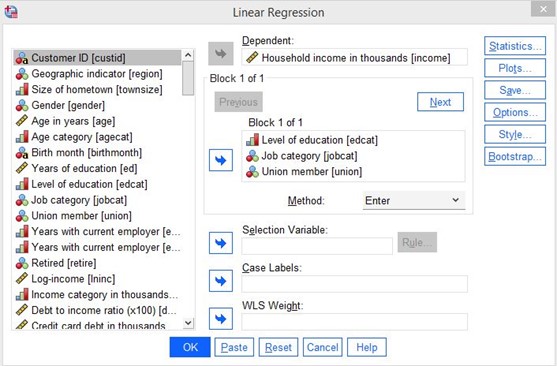
Figura 25: Selecția variabilelor
În acest exemplu, vom face o analiză de regresie multiplă. Vom examina efectele nivelului de educație, categoriilor de locuri de muncă și apartenenței la sindicat asupra venitului gospodăriei.
Înainte de a începe, aș dori să vă reamintesc că variabilele ar trebui să fie distribuite în mod normal și să aibă o varianță egală.
După ce ați selectat variabilele, faceți clic pe butonul Statistici din dreapta:
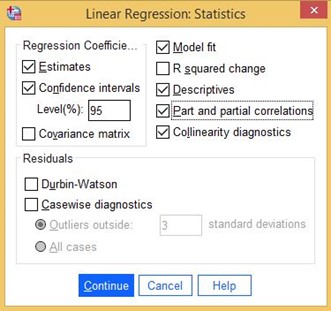
Figura 26: Statistici și specificații
Selectați potrivirea modelului, descriptive, corelații parțiale și parțiale, diagnosticarea colinearității, intervale de încredere (ca 95%) și faceți clic pe Continuare.
În meniul principal, faceți clic pe OK pentru a continua analiza.
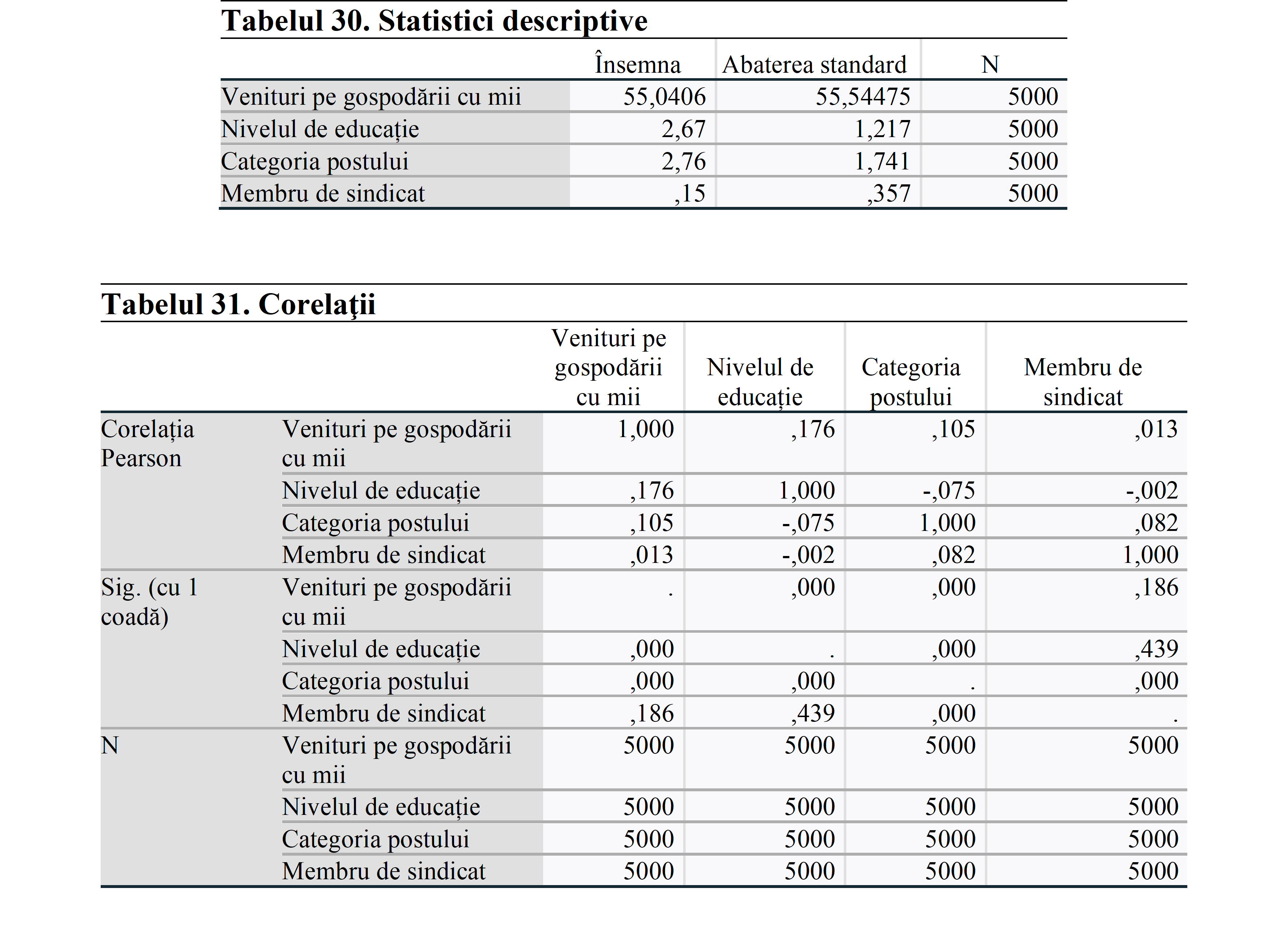
În matricea de corelație, este important să nu aveți o relație peste 0,70. Acest lucru indică o relație puternică între variabile și produce rezultate false. Acest lucru ar indica o problemă de multicolinearitate. În această analiză, vedem că nu există o relație puternică între variabile. Deci, putem continua să analizăm.
Rezumatul modelului arată valorile R. Deoarece am folosit un model de regresie multiplă, trebuie să verificăm R pătrat ajustat. Această valoare arată puterea variabilelor independente de a explica variabila dependentă. Deci, din nivelul de educație, categoria de locuri de muncă și apartenența la sindicat, doar 4,4% din venitul gospodăriei poate fi explicat. Aceasta înseamnă că există și alți contribuitori pe care nu îi putem observa și folosi în prezent în model. Dacă aveți mai multe variabile, trebuie să le utilizați în modelul de regresie, altfel analiza va fi efectuată de variabile neobservate.
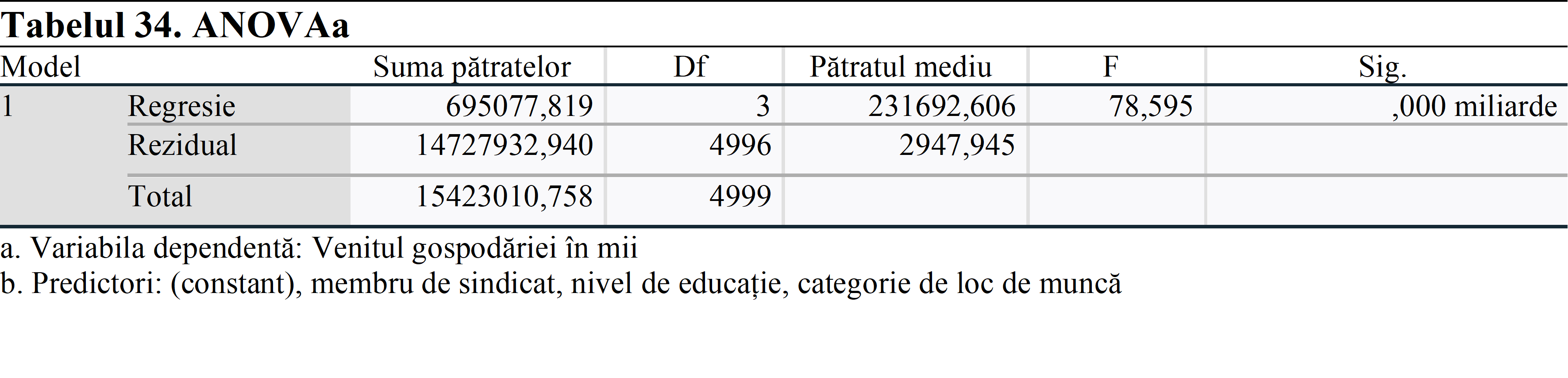
Când am verificat Sig. (valoarea p) a analizei ANOVA, se poate observa că este mai mică de 0,05. Aceasta înseamnă că cel puțin o variabilă dintre variabilele independente are un efect semnificativ statistic asupra variabilei dependente. Pentru mai multe informații despre efect, vom examina următoarea analiză.
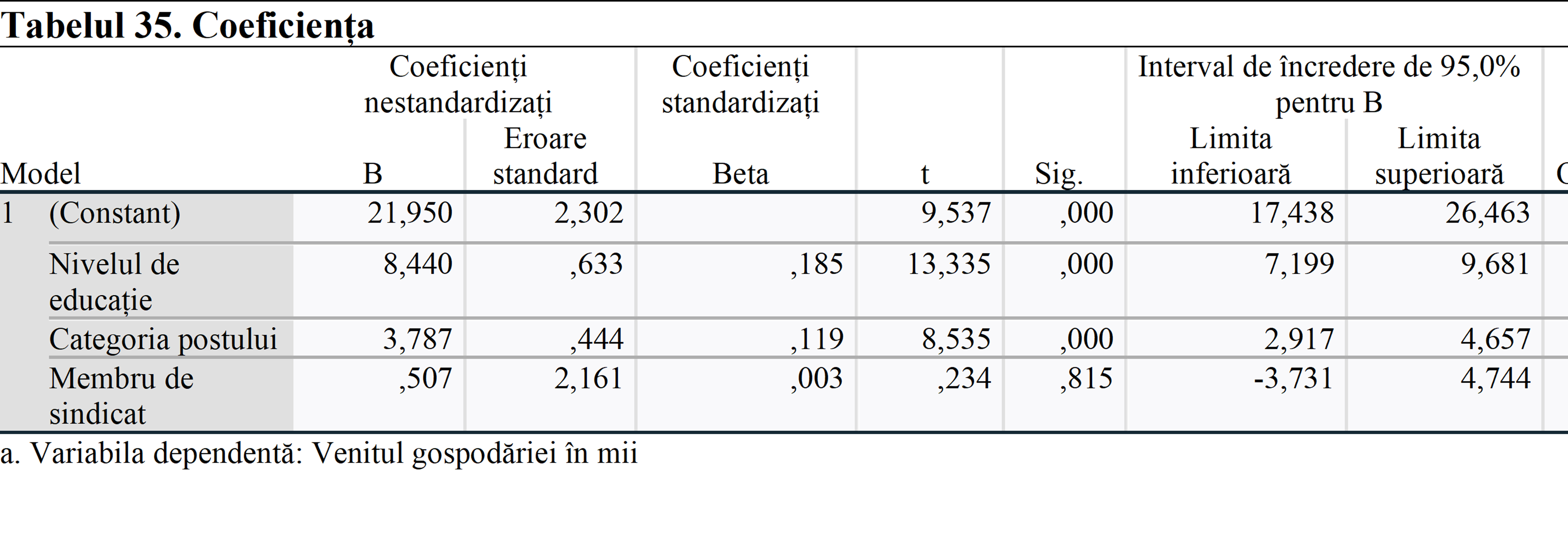
Primul lucru pe care trebuie să-l verificăm în acest tabel este Sig. (valoare p). Se poate observa că nivelul de educație și categoria de locuri de muncă au un efect semnificativ asupra venitului gospodăriei, pe de altă parte, a fi membru de sindicat nu are un impact semnificativ statistic asupra acestuia.
Coeficienții nestandardizați arată efectul creșterii unei unități asupra venitului gospodăriei. Deci, o creștere la nivel al nivelului de educație și a categoriei de locuri de muncă crește venitul gospodăriei cu 8.440 și 3.787 USD.
Coeficienții standardizați arată efectul unei unități de creștere a deviației standard asupra abaterii standard a venitului gospodăriei.
