
Korelaciona i regresiona analiza se koriste za ispitivanje povezanosti varijabli, a T-test i ANOVA analize za ispitivanje razlika među grupama.
Korelaciona analiza pokazuje povezanost svake varijable sa svakom od ostalih varijabli pojedinačno. Koeficijent povezanosti može biti negativan ili pozitivan. Za razliku od regresione analize, među varijablama ne može postojati uzročna veza.
Za ovaj primer koristićemo bazu podataka u SPSS programu: customer_dbase.sav
Kliknite na customer_dbase.sav.
Kliknite na opciju Analyze na meniju na vrhu ekrana.
Pronađite Correlate u okviru opcije Analyze. Potom klinite na dugme Bivariate Correlations.
Kada kliknete, pojaviće se sledeći meni:

Za korelacionu analizu važna je pretpostavka o normalnosti distribucije. Ukoliko su varijable normalno distribuirane, preba da koristite Pirsonov koeficijent korelacije, a ako nisu, koristite Spirmanov koeficijent korelacije.
Ako pretpostavite da postoji samo jedan smer povezanosti među varijablama (tj. očekujete samo pozitivnu korelaciju među varijablama), treba da odaberete One-tailed test. Ako niste sigurni ili ne očekujete samo pozitivnu ili samo negativnu povezanost, odaberite Two-tailed test.
Kada završite, kliknite OK da vidite rezultate. U ovom primeru odabrali smo i Pirsonov i Spirmanov koeficijent.

Ako je prisutna oznaka *, to znači da je korelacija značajna na nivou 0,05.
Rezultati analize pokazuju da postoji negativna korelacija između Credit card debt (Zaduženje po kreditnoj kartici) i Number of people in household (Broj ljudi u domaćinstvu), kao i da postoji pozitivna korelacija između Credit card debt (Zaduženje po kreditnoj kartici) i Household income (Prihodi po domaćinstvu). Može se reći da domaćinstva više zarađuju nego što troše. Zbog toga postoji povezanost.
Regresiona analiza se može koristiti za ispitivanje efekta nezavisne varijable ili nezavisnih varijabli na zavisnu varijablu. Prosta regresiona funksija se može prikazati na sledeći način:
Yi = ß0 + ß1x + ɛ
Yi: Zavisna varijabla
ß0: Konstanta / Presek
ß1: Nagib / Koeficijent
x: Zavisna varijabla
ɛ: Greška
U analizi može biti više od jedne nezavisne varijable. Može se utvrditi koeficijent efekta svake od njih na zavisnu varijablu. Nezapaženi efekti i varijable obuhvaćeni su terminom Greške.
Za ovu vežbu koristićmo datoteku iz SPSS programa: customer_dbase.sav
Odaberite customer_dbase.sav.
Kliknite na Analyze opciju na vrhu stranice ekrana.
Pronađite Regression u okviru opcije Analyze. Zatim kliknite na opciju Linear. Kada kliknete, pojaviće se sledeći meni:

U ovom primeru uradićemo višestruku regresionu analizu. Ispitaćemo efekte varijabli Level of education (Nivo obrazovanja), Job category (Kategorija zaposlenja) i Union member (Članstvo u sindikatu) na varijablu Household income (Prihod domaćinstva).
Pre nego što počnemo, želimo da vas podsetimo da vaše varijable treba da imaju normalnu distribuciju i jednake varijanse. Kada odaberete varijable, kliknite na dugme Statistics na desnoj strani:

Odaberite: Model fit, Descriptives, Part and partial correlations, Colinearity diagnostics, Confidence intervals (95%) i kliknite na Continue.
Na glavnom meniju klinite OK da biste nastavili analizu.
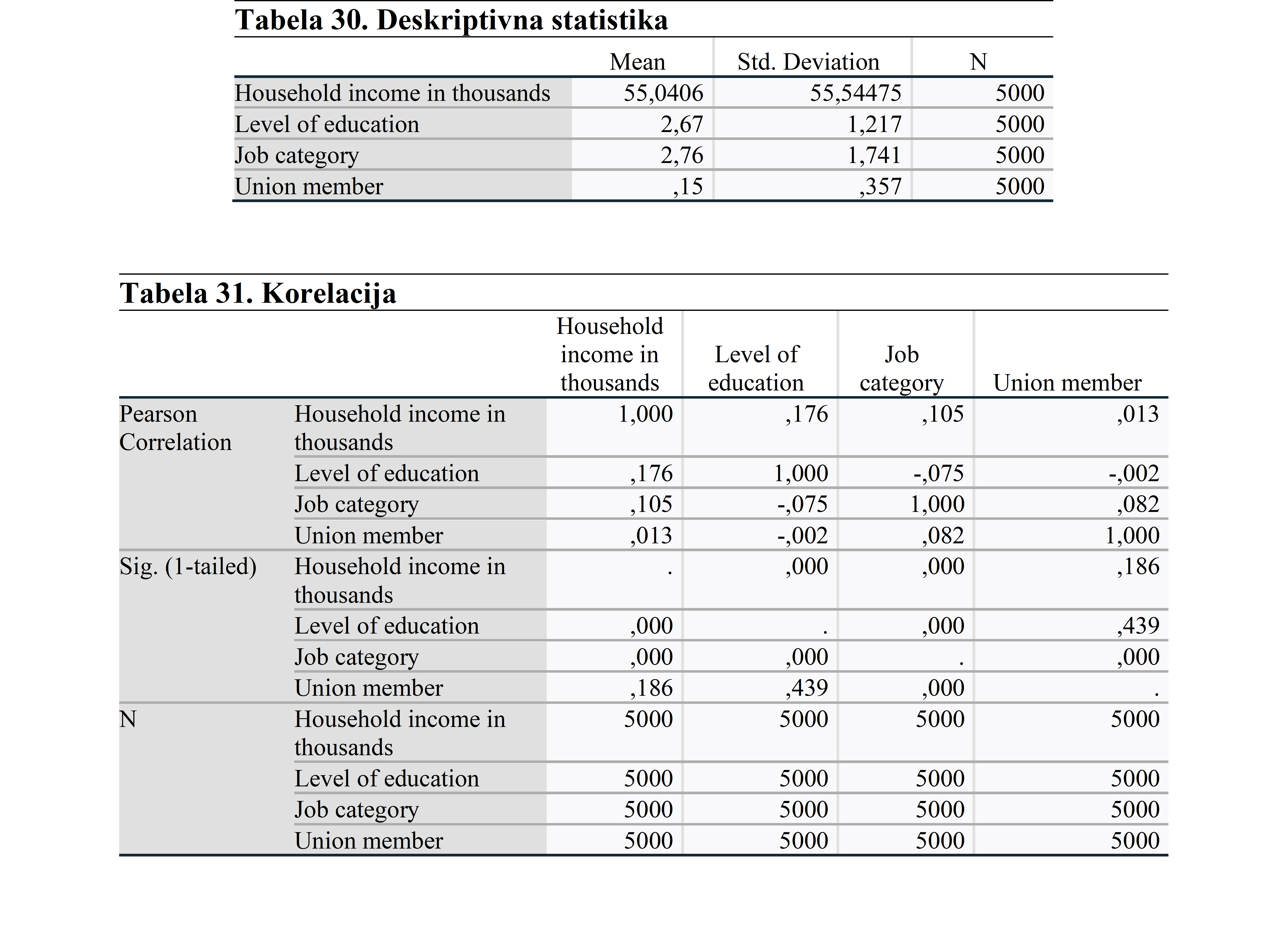
U matrici korelacija važno je da nema vrednosti iznad 0,70. To ukazuje na jaku vezu između varijabli i daje lažne rezultate. To bi ukazivalo na problem multikolinearnosti. U ovoj analizi vidimo da ne postoji jaka veza između varijabli. Dakle, možemo da nastavimo sa analizom.

Rezime modela prikazuje R-vrednosti. Pošto smo koristili model višestruke regresije, moramo da proverimo Adjusted R Square. Ova vrednost pokazuje moć nezavisnih promenljivih da objasne zavisnu promenljivu. Dakle, na osnovu nivoa obrazovanja, vrste posla i članstva u sindikatu može se objasniti samo 4,4% prihoda domaćinstva. To znači da postoje i drugi činioci koje trenutno ne možemo posmatrati i koristiti u modelu. Ako imate više varijabli, potrebno je da ih koristite u regresionom modelu, inače će na analizu uticati neopažene varijable.
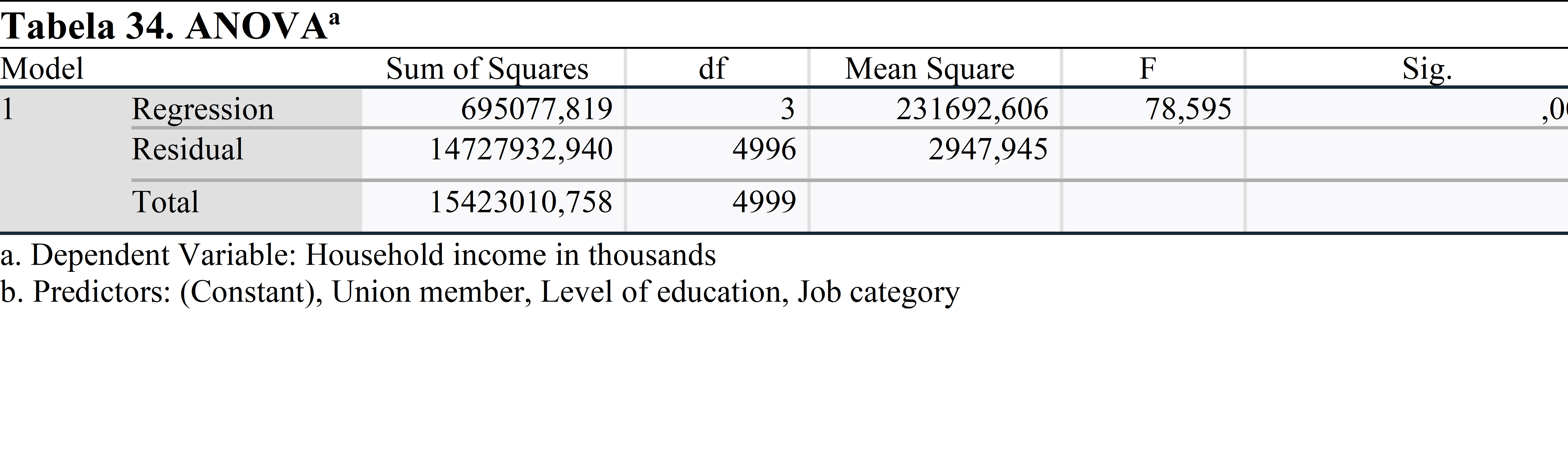
Kada proverimo vrednost Sig. (p-vrednost) analize ANOVA, videćemo da je niža od 0,05. To znači da najmanje jedna varijabla među nezavisnim varijablama ima statistički značajan uticaj na zavisnu varijablu. Više informacija o efektu dobićemo pomoću sledeće analize.

Prvo što treba da proverimo u tabeli je vrednost Sig. (p-vrednost). Može se videti da nivo obrazovanja i kategorija zaposlenja imaju značajan efekat na prihode domaćinstva, dok članstvo u sindikatu nema.
Nestandardizovani koeficijent (Unstandardised Coefficient) pokazuje efekat povećanja za jednu jedinicu na prihod domaćinstva. Dakle, povećanje nivoa obrazovanja i kategorije zaposlenja za jedan nivo povećava prihod domaćinstva za 8,440, odnosno 3,787 USD.
Standardizovani koeficijent (Standardised Coefficient) pokazuje efekat povećanja za jednu jedinicu na standardnu devijaciju prihoda domaćinastva.