Özet: SPSS kullanarak korelasyon ve regresyon analizi ile uygulamalı pratik.
Öğrenme Hedefleri:
SPSS kullanarak korelasyon ve regresyon analizleri yapma ve sonuçları yorumlama konusunda pratik deneyim kazanın.
Korelasyon analizini kullanarak değişkenler arasındaki ilişkileri nasıl değerlendireceğinizi ve regresyon analizini kullanarak tahmin modelleri oluşturmayı öğrenin.
Korelasyon ve regresyon analizlerinden elde edilen çıktıları yorumlama ve sonuçlara dayalı sonuçlar çıkarma pratiği yapın.
Korelasyon ve regresyon analizleri, değişkenler arasındaki ilişkiyi incelerken, T-testi ve ANOVA tipi analizler gruplar arasındaki farkları inceler.
Korelasyon analizi, her bir değişkenin birbirleriyle olan ilişkisini ayrı ayrı gösterir. Değişkenler arasındaki ilişkinin katsayısı negatif veya pozitif olabilir. Regresyon analizinin aksine, değişkenler arasında nedensellik olmayabilir.
Bu örnek için SPSS örneklerinden customer_dbase.sav veri setini kullanacağız.
customer_dbase.sav dosyasını seçin.
Üst menüden Analyze bölümüne tıklayın.
Analyze altında Correlate bölümünü bulun. Ardından Bivariate Correlations düğmesine tıklayın.
Tıkladığınızda aşağıdaki menüyü göreceksiniz:
Normallik varsayımı korelasyon analizi için önemlidir. Bu nedenle, değişkenleriniz normal dağılım gösteriyorsa pearson korelasyon katsayısını, değilse spearman katsayısını kullanmanız gerekir.
Değişkenler arasında tek yönlü bir ilişki olduğunu varsayıyorsanız (yani, sadece pozitif bir ilişki bekliyorsanız), One-tailed testi seçmelisiniz. Eğer emin değilseniz veya pozitif ya da negatif ilişki öngörmüyorsanız, Two-tailed testi seçmelisiniz.
İşinizi bitirdiğinizde, sonuçları görmek için OK düğmesine tıklayın. Bu örnek için hem Pearson hem de Spearman Katsayılarını seçtik.
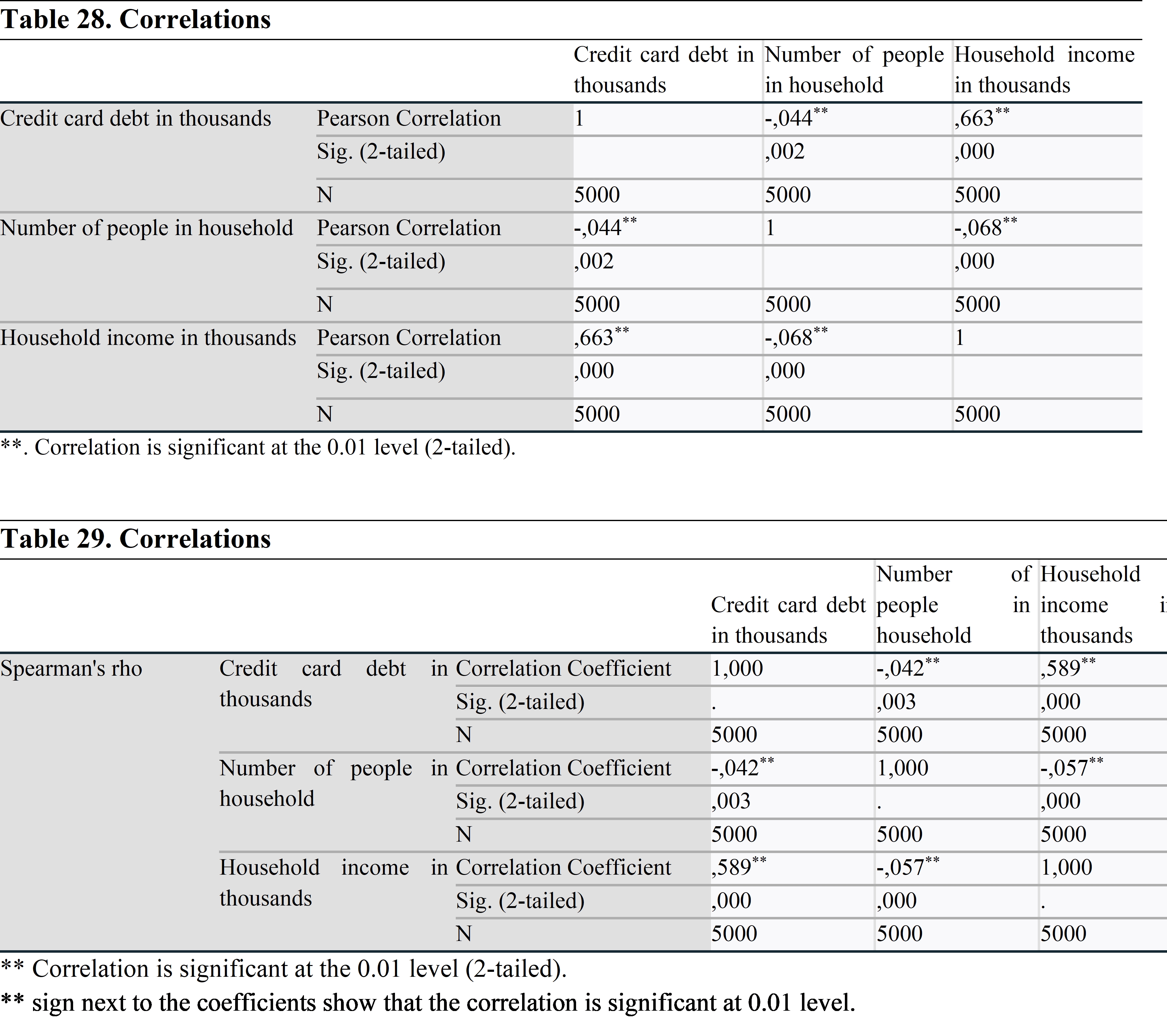
İşaret * ise, bu, korelasyonun 0.05 düzeyinde anlamlı olduğu anlamına gelir.
Her iki katsayı testinde de her bir değişken çifti arasında istatistiksel olarak anlamlı ilişki vardır.
Analiz sonuçları, kredi kartı borcu ile hanedeki kişi sayısı arasında negatif, kredi kartı borcu ile hane halkı geliri arasında pozitif yönlü bir ilişki olduğunu göstermektedir. Hanehalkının harcadığından daha fazla gelir elde ettiğini söyleyebiliriz. Böyle bir ilişkinin olmasının nedeni budur.
Regresyon analizi, bağımsız değişken(ler)in bağımlı değişken üzerindeki etkisini incelemek için kullanılabilir. Basit bir regresyon fonksiyonu: cYi = ß0 + ß1x + ɛ
Yi: Bağımlı değişken
ß0: Sabit / Kesişim Noktası
ß1: Eğim / Katsayı
an be illustrated as follows:
Yi = ß0 + ß1x + ɛ
Yi: Bağımlı değişken
ß0: Sabit / Kesişim Noktası
ß1: Eğim / Katsayı
x: Bağımsız değişken
ɛ: Hata terimi
Analizde birden fazla bağımsız değişken olabilir. Her değişkenin bağımlı değişken üzerindeki etkileri katsayıları ile incelenebilir. Gözlemlenmeyen etkiler ve değişkenler hata terimi ile temsil edilecektir.
Bu örnek için SPSS örneklerinden customer_dbase.sav veri setini kullanacağız.
customer_dbase.sav dosyasını seçin.
Üst menüden Analyze bölümüne tıklayın.
Analyze altında Regression bölümünü bulun. Ardından Linear düğmesine tıklayın.
Tıkladığınızda aşağıdaki menüyü göreceksiniz:
Bu örnekte çoklu regresyon analizi yapacağız. Eğitim düzeyinin, iş kategorilerinin ve sendika üyeliğinin Hanehalkı geliri üzerindeki etkilerini inceleyeceğiz.
Başlamadan önce, değişkenlerinizin normal dağılım göstermesi ve eşit varyansa sahip olması gerektiğini hatırlatmak isterim.
Değişkenlerinizi seçtikten sonra, sağdaki Statistics düğmesine tıklayın.
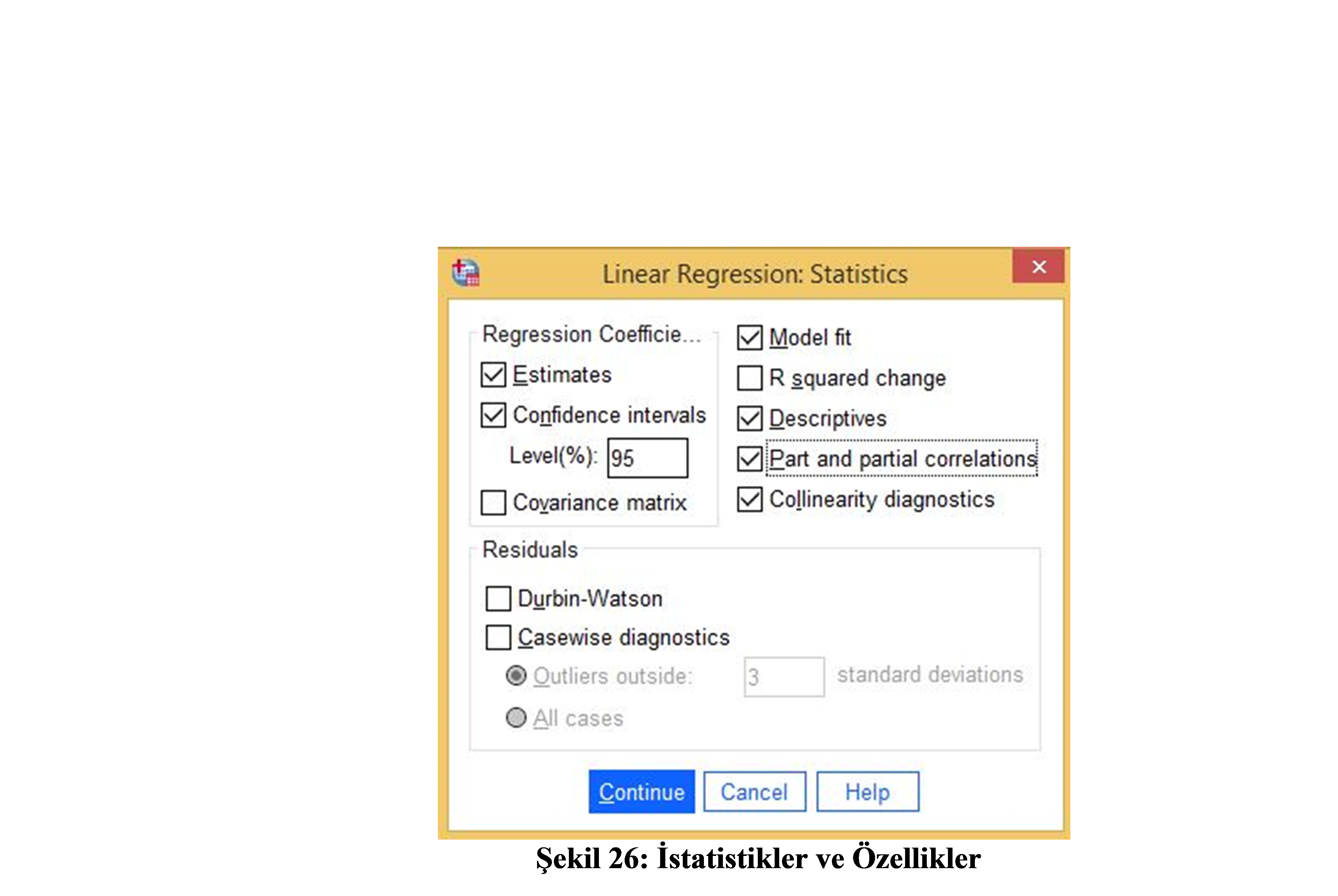
Model fit, descriptives, part and partial correlations, colinearity diagnostics, confidence intervals (95%) seçeneklerini seçin ve Continue düğmesine tıklayın.
Ana menüde, analize devam etmek için OK düğmesine tıklayın.
Korelasyon matrisinde, 0.70'in üzerinde bir ilişkiye sahip olmamak önemlidir. Bu, değişkenler arasında güçlü bir ilişki olduğunu ve yanıltıcı sonuçlar verebileceğini gösterir. Bu durum, çoklu bağlantı (multicolinearity) problemini işaret eder. Bu analizde, değişkenler arasında güçlü bir ilişki olmadığını görüyoruz. Dolayısıyla, analize devam edebiliriz.
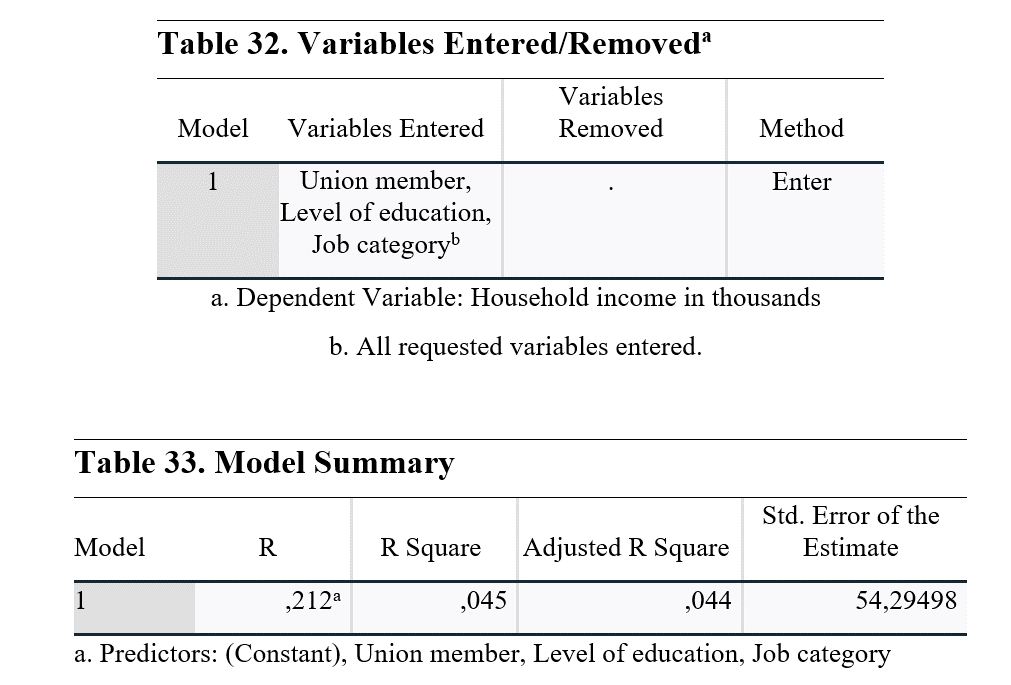
Model özeti R değerlerini gösterir. Birden fazla regresyon modeli kullandığımız için Adjusted R Square değerini kontrol etmemiz gerekmektedir. Bu değer, bağımsız değişkenlerin bağımlı değişkeni açıklama gücünü gösterir. Eğitim seviyesi, iş kategorisi ve sendika üyeliğinden, hanehalkı gelirinin sadece %4.4'ü açıklanabilir. Bu, modelde şu anda gözlemleyemediğimiz ve kullanamadığımız başka katkı sağlayan faktörlerin olduğunu gösterir. Daha fazla değişkeniniz varsa, bunları regresyon modelinde kullanmanız gerekir, aksi takdirde analiz gözlemlenmeyen değişkenlerden etkilenecektir.
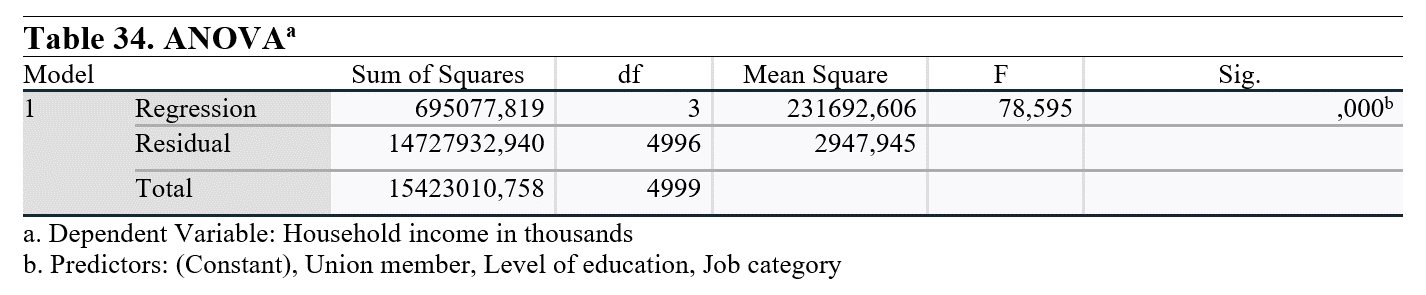
ANOVA analizinin Sig. (p-değeri) kontrol edildiğinde, 0.05'ten düşük olduğu görülmektedir. Bu, bağımsız değişkenler arasında en az bir değişkenin bağımlı değişken üzerinde istatistiksel olarak anlamlı bir etkisi olduğu anlamına gelir. Etki hakkında daha fazla bilgi için bir sonraki analizi inceleyeceğiz.
Bu tabloda kontrol etmemiz gereken ilk şey Sig. (p-değeri) dir. Eğitim seviyesi ve iş kategorisinin hanehalkı geliri üzerinde anlamlı bir etkisi olduğu görülmektedir, diğer yandan sendika üyesi olmanın istatistiksel olarak anlamlı bir etkisi yoktur.
Standardize edilmemiş katsayılar, bir birim artışın hanehalkı geliri üzerindeki etkisini gösterir. Dolayısıyla, eğitim seviyesindeki bir seviye artışı hanehalkı gelirini 8,440 USD ve iş kategorisindeki bir seviye artışı hanehalkı gelirini 3,787 USD artırır.
Standardize edilmiş katsayılar, standart sapmadaki bir birim artışın hanehalkı gelirinin standart sapması üzerindeki etkisini gösterir.
